二分
简述
在ACM竞赛中,或者说在程序员的码代码生涯中,二分作为一种基础的、能降低时间复杂度的算法,是我们必须要掌握的,也必须要熟练掌握,下面我们先通过下面这个小问题来了解什么是二分。
问题
我们定义所谓的 Special Number是指满足以下条件的数:
- 该数里面每一个数字都不能重复,譬如123算是S.N.,而122就不算。
- 该数不能有前导0,譬如01不算S.N,而1就是S.N。
多组测试数据(大概20000组),每组测试数据给出你一个n(n <= 10,000,000),现在问你比n小的Special Number有多少个。
怎么做?
看了上一节书的同学,应该很容易想到使用枚举,我们可以枚举1~n-1(至于为什么不是从0开始,是因为……请认真看题~),判断每一个数字是不是S.N。
但是考虑极端情况,在多组测试数据中n都是10,000,000。而给的时间只有1s,所以如果你用之前学过的枚举,毫无疑问就超时了…因为时间复杂度是O(n)。然而我们有一种新的方法来解决这道题,就是二分。
初涉二分
回顾高中学过的知识,如果求一个单调递增或者单调递减的函数与x轴的交点,即 时 的值,
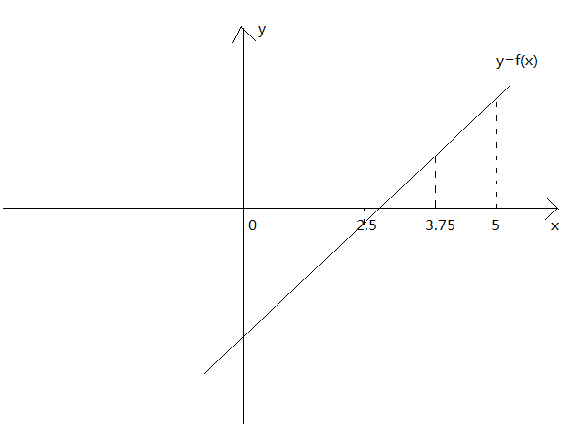
我们知道 , ,那么, 与x轴的交点的横坐标一定落在区间 内,这时我们取x为0和5的中值,即2.5,发现 ,那么 与x轴的交点的横坐标一定落在区间 内,同理,我们取新的x为2.5和5的中值,发现 ,那么 与x轴的交点的横坐标一定落在区间 内......如此往复,我们得到的答案就会越来越逼近交点。
这就是二分算法:通过不断检测左端点和右端点f(x)是否满足题意来减少未知数x的取值范围。这样最后肯定会不断逼近正确答案,直到最终左右端点非常靠近,端点值就是答案。
设计算x次能够得到答案,n是取值范围大小,即右端点-左端点。那么=n,即经过x次二分可以得到n。 所以二分的时间复杂度是log(n),计算机里log(n)就表示log(n),所以时间复杂度是O(log(n))。
回到我们刚才的问题,我们可以先预处理出来1~10,000,000里面的所有Special Number。然后二分这些S.N,直到找到第一个比n小的S.N,就可以知道答案了。代码如下:
#include <stdio.h>
#include <cstring>
#include <algorithm>
using namespace std;
int arr[1000000];
bool check(int x)
{
bool vis[10], flag = true;
///flag作为哨兵变量出现,她用来监视这个数是不是有重复数字
memset(vis, false, sizeof(vis)); ///memset是初始化函数,用于把数组初始化为某个值
while (x) { ///这个while的作用是把给出的数分解出来,然后一个个判断是否出现过..例如:1234分解成1,2,3,4
int tmp = x%10;
x /= 10;
if (vis[tmp]) {
flag = false; ///如果有重复的数字就把哨兵变量标记为false
break;
}
vis[tmp] = true;
}
return flag;
}
int n;
bool ok(int x)
{
return arr[x] < n;
}
int main()
{
int tot = 0;
for (int i = 1; i <= 10000000; ++i) { ///把范围内的符合答案的值都求出来
if (check(i)) {
arr[tot++] = i;
}
}
//printf("_%d\n", tot);
while (~scanf("%d", &n)) {
int r = tot-1, l = 0, mid, res;///把左右边界初始化
if (n <= 1) {
puts("0");
continue;
}
while (l <= r) {
mid = (l+r)/2;
if (arr[mid] < n) {
l = mid+1;
res = mid;
} else {
r = mid-1;
}
}
printf("%d\n", res+1);///因为我们的左边是从0开始的,所以要+1
}
return 0;
}
模版
普通二分模版
int l,r,res; //l, r初始化,问题答案的左边界和右边界的确定 while(l<=r){ int mid=(l+r)/2; if (ok(mid)){ res=mid; r= mid-1; } else l=mid+1; }但是除去常见的二分题目,还有一种需要大家注意的:浮点数型二分, 因为整数型二分当(l+r)/2的时候是向下取整,所以为了避免出现l=3,r=4,然后mid=(3+4)/2=3的情况(会造成无限循环),所以整数型二分l=mid+1, 而浮点数型就不需要, 看一下模板:
浮点数二分模版
const double eps = 1e-7; double l, r; // l,r初始化,问题答案的左边界和右边界的确定 while (l + eps < r){ double mid = (l + r) / 2.0; if (ok (mid)){ l = mid; // r = mid; } else { r = mid; // l = mid; } }
例题
例题1.hrbust 1530
题意:小M要举行Party,她有n个pie,已知每个pie的半径,问若要分给k个好朋友同等份的pie,每个好朋友最多可以拿多大的pie?每个好朋友得到的同等份的pie只能来自同一个pie。P.S..小M也想要分得一块同等份的pie..(答案精确到小数点后四位)
要求:Time Limit: 1000 MS , Memory Limit: 65535 K
思路:这道题的题意有点难理解,其实可以简化一下,就是有k+1个人,有 n个pie,每个pie的大小都是已知的,问每个人最多能分得多大的pie?例如pie大小为1,2,3。则如果每个人最多分得大小为2的pie,则最多分给两个人。
- 我们可以用二分,二分的是每个人可分得的pie的大小,这样最后就可以算出总共可以分给几个人,以此来逼近答案。
- 初始化的时候l=0,r=最大的pie的大小(π*),为了防止精度问题,我们最后才乘以π,表示最少每个人都没pie吃,最多每个人占据一个最大的pie。
代码:
#include <stdio.h>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
#define eps 1e-8 ///定义精度值10^-8
#define pi acos(-1) ///定义pi值
int n, k;
int arr[10010];
int ok(double x)
{
int ans = 0;
for (int i = 0; i < n; ++i)
ans += (int)arr[i]/x; ///算出每一个pie按照x大小分可以分为几份
///然后累加起来,看一下所有pie按照每份大小为x的时候总共可以得到几份
return ans;
}
int main()
{
int nCase;
double l, r, mid;
scanf("%d", &nCase);
while (nCase--) {
scanf("%d %d", &n, &k);
l = r = 0; ///左边界定义为0,表示最少每个人得到大小为0的pie
///右边界定义为0,是为了到时候得出pie的最大值
for (int i = 0; i < n; ++i) {
scanf("%d", &arr[i]);
arr[i] *= arr[i]; ///理论上我们应该算出每个pie的r*r*π
///但是为了防止计算的时候出现精度误差,我们只计算r*r,最后才乘以π
r = max(r, (double)arr[i]); ///得到最多拿到的pie的大小,那就是最大的那个pie的大小
}
// printf("%.4lf %.4lf\n", l, r);
while (l+eps < r) {
mid = (l+r)/2.0;
if (ok(mid) >= k+1) l = mid;
else r = mid;
}
printf("%.4lf\n", pi*l); ///用结果的r*r*π得到得到的pie的最终大小
}
return 0;
}
例题2.hdu 4282
题意:。告诉我们K的大小,问符合这个等式的X,Y,Z的组合有多少种。
要求:Time Limit: 2000 MS , Memory Limit: 32768 K
错误思路:看到这道题,首先我们应该想到的是枚举,代码如下。但是观察K的范围和时限,枚举显然会超时。
int count=0;
for(long long x=0;x<=k;x++)
for(long long y=x+1;y<=k;y++)
for(long long z=2;z<=31;z++)
if(pow(x*1.0,z*1.0)+pow(y*1.0,z*1.0)+x*y*z==k)
count++;
printf("%d\n",count);
这样做会超时,那我们应该怎么做?这一节我们讲的是二分,大家不妨向二分方向考虑一下。
正确思路:因为幂次的增长速度比较快,我们可以枚举X和Z,这样我们可以把三重循环降低到二重循环,然后二分搜索每一对(X,Z)是否存在对应的Y。对于A的B次方我们可以先打表储存,使用的时候直接调用,这样也可以降低一定的时间复杂度。代码如下:
#include<cstdio>
#include<cstring>
using namespace std;
#define LL long long
LL mat[50001][32]={0};
bool ok(int x,int z,int cnt)
{
int l=x+1,r=50000,mid;
for(;l<=r;)
{
mid=(l+r)>>1;
if(mat[mid][z]==0)
{
r=mid-1;
continue;
}
if(mat[mid][z]+x*mid*z<cnt)
l=mid+1;
else if(mat[mid][z]+x*mid*z>cnt)
r=mid-1;
else
return true;
}
return false;
}
int main()
{
int k;
for(int i=1;i<=50000;++i)
{
mat[i][1]=i;
for(int j=2;j<=31;++j)
{
mat[i][j]=mat[i][j-1]*i;
if(mat[i][j]>2147483648LL)
break;
//这个2147483648LL中的LL一定要加上
}
}
while(scanf("%d",&k)!=EOF)
{
if(k==0)
return 0;
long long summ=0;
int cnt;
for(int x=1;x<=50000&&x<=k;++x)
for(int z=2;z<=31;++z)
{
if(mat[x][z]==0)
break;
cnt=k-mat[x][z];
if(cnt-x*z<=0)
break;
if(ok(x,z,cnt))
summ++;
}
printf("%I64d\n",summ);
//这里的I64d和lld是一个意思
}
return 0;
}