排序

简述

学习计算机的任何一门语言，都要掌握排序算法，参与竞赛更要掌握排序算法，将来找工作笔试面试的时候都会考到排序算法，所以说排序算法是十分重要的，我们要全面掌握并深入理解。

分类及比较

1.冒泡排序

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

void bubble_sort(int arry[], int left, int right) {
    for(int i = left; i < right; i++) {
        for(int j = i; j < right; j++) {
            if(arry[j] > arry[j + 1]) {
                swap(arry[j], arry[j + 1]);
            }
        }
    }
}

时间复杂度：$O(n^2)$，空间复杂度：$O(n)$。

2.选择排序

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

void swap(int &a, int &b) {
    int tmp = a;
    a = b;
    b = tmp;
}

void select_sort(int arry[], int left, int right) {
    for(int i = left; i < right; i++) { 
        int Min = i;
        for(int j = i + 1; j <= right; j++) {
            if(arry[Min] > arry[j]) {
                Min = j;
            }
        }
        if(Min != i) {
            swap(arry[i], arry[Min]);
        }
    }
}

时间复杂度：$O(n^2)$，空间复杂度：$O(n)$。

3.直接插入排序

插入排序（Insertion Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用inplace排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

void insert_sort(int arry[], int left, int right) {
    for(int i = left + 1; i <= right; i++) {
        int tmp = arry[i];
        int j = i - 1;
        while(j >= left && arry[j] > tmp) {
            arry[j + 1] = arry[j];
            j--;
        }
        arry[j + 1] = tmp;
    }
}

时间复杂度：$O(n^2)$，空间复杂度：$O(n)$。

4.快速排序

快速排序是各种笔试面试中常出的一类题型，其基本思想是：从序列中选取一个作为关键字，对序列排一次序，使得关键字左侧的数都比关键字小，右侧的都大于等于关键字（左右两侧的序列依然是无序的），然后 将左侧的序列按照同样的方法进行排序，将右侧序列也按照同样的方法排序，已达到整个序列有序。

void quick_sort(int arry[], int left, int right) {
    if(left >= right) return ;
    int i = left, j = right;
    int tmp = arry[left];
    do {
        while(arry[j] > tmp && i < j) {
            j--;
        }
        if(i < j) {
            arry[i] = arry[j];
            i++;
        }
        while(arry[i] < tmp && i < j) {
            i++;
        }
        if(i < j) {
            arry[j] = arry[i];
            j--;
        }
    } while(i != j);
    arry[i] = tmp;
    quick_sort(arry, left, i - 1);
    quick_sort(arry, i + 1, right);
}

时间复杂度：$O(n\log n)$；空间复杂度：$O(n)$。

5.堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

void Heap_just(int a[], int root, int heap_size) {
    if(root < heap_size) {
        int Min = root;
        int l_son = root << 1 | 1;
        int r_son = (root << 1) + 2;
        if(l_son < heap_size && a[Min] > a[l_son]) Min = l_son;
        if(r_son < heap_size && a[Min] > a[r_son]) Min = r_son;
        if(Min == root) return ;
        a[root] ^= a[Min];
        a[Min] ^= a[root];
        a[root] ^= a[Min];
        Heap_just(a, Min, heap_size);
    }
}

void build_heap(int a[], int n) {
    for(int i = n / 2; i >= 0; i--) {
        Heap_just(a, i, n);
    }
}

void Heap_sort(int a[], int n) {
    build_heap(a, n);
    for(int i = n - 1; i > 0; i--) {
        a[i] ^= a[0];
        a[0] ^= a[i];
        a[i] ^= a[0];
        Heap_just(a, 0, i);
    }
}

时间复杂度：$O(n\log n)$。

6.桶排序

桶排序 (Bucket sort)或所谓的箱排序，是一个排序算法，工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。 桶排序是稳定的，且在大多数情况下常见排序里最快的一种,比快排还要快，缺点是非常耗空间,基本上是最耗空间的一种排序算法，而且只能在某些情形下使用。

实现步骤：

1. 设置一个定量的数组当作空桶子。
2. 寻访串行，并且把项目一个一个放到对应的桶子去。
3. 对每个不是空的桶子进行排序。
4. 从不是空的桶子里把项目再放回原来的串行中。

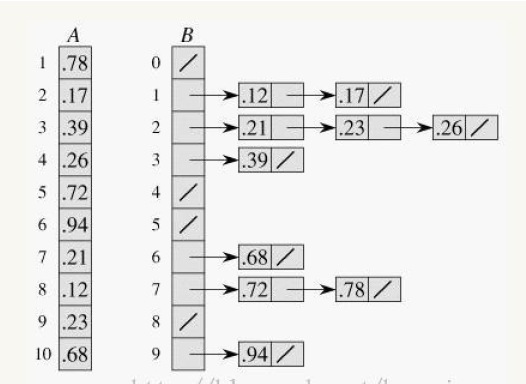
桶排序没有固定代码。
时间复杂度：$O(n)$。

7.归并排序

归并排序是一种稳定的算法，采用分治的思想，有序的子序列合并得到有序序列。

实现步骤：

1. 将序列分成长度为 n/2的两部分
2. 对于左右两部分采用分治的方法得到有序序列
3. 将左右两个有序序列合并得到整个有序序列

void arry_add(int arry[], int left, int mid, int right) {
    if(left >= right) return ;
    int i = left, j = mid + 1, k = 0;
    while(i <= mid && j <= right) {
        if(arry[i] <= arry[j]) {
            tmp[k++] = arry[i++];
        } else {
            tmp[k++] = arry[j++];
            cnt += (mid - i + 1);
        }
    }
    while(i <= mid) {
        tmp[k++] = arry[i++];
    } 
    while(j <= right) {
        tmp[k++] = arry[j++];
    }
    for(i = 0; i < k; i++) {
        arry[i + left] = tmp[i];
    }
}
void merge_sort(int arry[], int left, int right) {
    if(left >= right) return ;
    int mid = (left + right) >> 1;
    merge_sort(arry, left, mid);
    merge_sort(arry, mid + 1, right);
    arry_add(arry, left, mid, right);
}

时间复杂度：$O(n\log n)$。

8.二分插入排序

二分（折半）插入（Binary insert sort)排序是一种在直接插入排序算法上进行小改动的排序算法。其与直接排序算法最大的区别在于查找插入位置时使用的是二分查找的方式，在速度上有一定提升。

void Binary_Insert_sort(int arry[], int first, int end) {
    for(int i = first + 1; i <= end; i++) {
        int low = first, high = i - 1;
        while(low <= high) {
            int mid = (low + high) >> 1;
            if(arry[mid] > arry[i]) {
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        int key = arry[i];
        for(int j = i; j > high + 1; j--) {
            arry[j] = arry[j - 1];
        }
        arry[high + 1] = key;
    }
}

时间复杂度：$O(n^2)$，空间复杂度：$O(n)$。

9.希尔排序

希尔排序，也称递减增量排序算法，因DL．Shell于1959年提出而得名，是插入排序的一种高速而稳定的改进版本。

实现步骤：

1. 先取一个小于$n$的整数$d1$作为第一个增量，把文件的全部记录分成$d1$个组。
2. 所有距离为$d1$的倍数的记录放在同一个组中，在各组内进行直接插入排序。
3. 取第二个增量$d2<d1$重复上述的分组和排序。
4. 直至所取的增量$dt=1$，即所有记录放在同一组中进行直接插入排序为止。

void shell_sort(int arry[], int left, int right) {
    int n = right - left;
    int gep = 1;
    while(gep <= n) {
        gep = gep << 1 | 1;
    }
    while(gep >= 1) {
        for(int i = left + gep; i <= right; i++) {
            int temp = arry[i];
            int j = i - gep;
            while(j >= left && arry[j] > temp) {
                arry[j + gep] = arry[j];
                j -= gep;
            }
            arry[j + gep] = temp;
        }
        gep = (gep - 1) / 2;
    }
}

时间复杂度：小于$O(n^2)$。

10.鸡尾酒排序

鸡尾酒排序等于是冒泡排序的轻微变形。不同的地方在于从低到高然后从高到低，而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的效能，原因是冒泡排序只从一个方向进行比对(由低到高)，每次循环只移动一个项目。

void swap(int &a, int &b) {
    int tmp = a;
    a = b;
    b = tmp;
}

void cocktail_sort(int arry[], int left, int right) {
    int i = left, j = right;
    bool isSwap = false;
    do {
        for(int k = i; k < j; k++) {
            if(arry[k] > arry[k + 1]) {
                swap(arry[k], arry[k + 1]);
            }
        }
        isSwap = false;
        j--;
        for(int k = j; k > i; k--) {
            if(arry[k] < arry[k - 1]) {
                swap(arry[k], arry[k - 1]);
                isSwap = true;
            }
        }
        i++;
    } while(i <= j && isSwap);
}

时间复杂度：小于$O(n^2)$且大于$O(n)$。

11.计数排序

计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。

实现步骤：

1. 找出待排序的数组中最大和最小的元素。
2. 统计数组中每个值为i的元素出现的次数，存入数组C的第i项。
3. 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）。
4. 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1 。

//只可以对非负数进行排序
int max(int a, int b) {
    return a > b ? a : b;
}

void count_sort(int arry[], int left, int right) {
    int Max = 0;
    int cnt = right - left + 1;
    for(int i = left; i <= right; i++) {
        Max = max(Max, arry[i]);
    }
    int *count = new int[Max + 1];
    int *tmp = new int[cnt + 1];
    for(int i = left; i <= right; i++) {
        ++count[arry[i]];
    }
    for(int i = 1; i <= Max; i++) {
        count[i] += count[i - 1];
    }
    for(int i = right; i >= left; i--) {
        tmp[count[arry[i]]--] = arry[i];
    }
    memcpy(arry + left, tmp + 1, (cnt)* sizeof(int));
    delete(count);
    delete(tmp);
}

时间复杂度：$O(n+k)$。

12.睡排序

//java 代码
class SortThread extends Thread{
    int ms = 0;
    public SortThread(int ms){
        this.ms = ms;
    }
    public void run(){
        try {
            sleep(ms*10+10);
        } catch (InterruptedException e) {
            // TODO Auto-generated catch block
            e.printStackTrace();
        }
        System.out.println(ms);
    }
}

竞赛中常用排序

1.库函数sort

• 头文件：#include<algorithm>
• 函数原型：sort(begin,end)或sort(begin,end,cmp)
• 实例

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

int a[5]={2,1,0,3,4};

int cmp1(int a,int b){
    return a>b;
}

int cmp2(int a,int b){
    return a<b;
}

void _print(){
    for(int i=0;i<5;i++)
        printf("%d ",a[i]);
    printf("\n");
}

int main(){
    sort(a,a+5);
    _print();
    //将输出0 1 2 3 4

    sort(a,a+5,cmp1);//使用cmp1函数中自定义的优先级进行排序
    _print();
    //将输出4 3 2 1 0

    sort(a,a+5,cmp2);//使用cmp2函数中自定义的优先级进行排序
    _print();
    //将输出0 1 2 3 4
}

2.结构体排序

这里我们也是用库函数sort，只不过需要该进一下自定义排序函数cmp。

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

struct A{
    int a,b;
}aa[5];

void init(){
    aa[0].a=3;
    aa[0].b=2;
    aa[1].a=2;
    aa[1].b=4;
    aa[2].a=2;
    aa[2].b=5;
    aa[3].a=2;
    aa[3].b=3;
    aa[4].a=1;
    aa[4].b=9;
}

int cmp1(A aa,A bb){
    if(aa.a==bb.a)
        return aa.b>bb.b;
    return aa.a>bb.a;
}

int cmp2(A aa,A bb){
    if(aa.a==bb.a)
        return aa.b<bb.b;
    return aa.a>bb.a;
}

void _print(){
    for(int i=0;i<5;i++)
        printf("%d %d\n",aa[i].a,aa[i].b);
}

int main(){
    init();

    sort(aa,aa+5,cmp1);
    //使用cmp1函数中自定义的优先级进行排序,先按a降序排序，a值相等则按照b值降序排序
    _print();
    /*将输出
        3 2
        2 5
        2 4
        2 3
        1 9
    */

    sort(aa,aa+5,cmp2);
    //使用cmp2函数中自定义的优先级进行排序,先按a降序排序，a值相等则按照b值升序排序
    _print();
    /*将输出
        3 2
        2 3
        2 4
        2 5
        1 9
    */
}