最长回文子串
有这样一种题,求一个字符串的最长回文子串的长度。
hdu 3608就是求最长回文子串的一道题
有这样几种解法
暴力法
枚举所有子串且每次判断该子串是否是回文子串,时间复杂度是 ,理所当然的T掉。
#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
const int maxa = 110000;
char str[maxa];
int main(){
while(scanf("%s", &str)!=EOF){
int ans = 0;
for(int i = 0; str[i]; i++){
for(int k = i+1; str[k]; k++){
int ok = 1;
for(int j = i; j <= (i+k)/2; j++){
if(str[j] != str[k-(j-i)]){
ok = 0;
break;
}
}
if(ok){
ans = max(ans, k-i+1);
}
}
}
printf("%d\n", ans);
}
}
枚举中心法
首先将字符串每个字符的两遍都加上特殊字符,变成新串,例如原串为abab,新串为#a#b#a#b#,然后以每个点为中心,求出以该点为中心的最长回文串的长度,枚举中心的时间复杂度是 ,枚举最长长度的时间复杂度是 ,总时间复杂度是 ,依旧超时。
#include<iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
const int maxa = 111111;
char a[maxa];
char str[maxa*2];
int main(){
while(scanf("%s", &a)!=EOF){
int ans = 0;
for(int i = 0; ; i++){
if(a[i]){
str[i*2] = '#';
str[i*2+1] = a[i];
}else{
str[i*2] = '#';
str[i*2+1] = 0;
break;
}
}
printf("%s\n", str);
int len = strlen(str);
for(int i = 0; str[i]; i++){
for(int j = 0; i-j >= 0 && i+j < len; j++){
if(str[i-j] == str[i+j]){
ans = max(ans, j);
}else break;
}
}
printf("%d\n", ans);
}
}
动态规划
for循环枚举所有子串,当 被枚举到的时候, 也一定被枚举到,dp[i][j]=1代表 是回文子串,只要str[i] == str[j]并且,dp[i+1][j-1]==1,那么dp[i][j]=1,时间复杂度为 ,空间复杂度也是 .
#include<iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
const int maxa = 1111;
char str[maxa];
int dp[maxa][maxa];
int main(){
while(scanf("%s", &str)!=EOF){
memset(dp, 0, sizeof(dp));
int l = strlen(str);
for(int i = 0; i < l; i++){
dp[i][i] = 1;
}
int ans = 0;
for(int j = 1; j < l; j++){
for(int i = 0; str[i]; i++){
if(i+j > l) break;
int k = i+j;
if(str[i] == str[k]){
if(i+1 > k-1 || dp[i+1][k-1]){
dp[i][k] = 1;
ans = max(ans, k-i+1);
}
}
}
}
printf("%d\n", ans);
}
}
Manacher算法
将字符串中的每个字符的左右都加上一个串中不会出现的特殊字符,例如字符串为abcde,那么变换后的串为#a#b#c#d#e#。我们称变换后的串为str2。
另p[i]为str2中第i个字符为中心的最长回文串的边界到中心的距离,i加上p[i],就是以i为中心的最长回文子串的右边界,用两个辅助变量分别是id,和mx。mx代表之前所有回文串最右右边界,id代表那最右右边界的点。
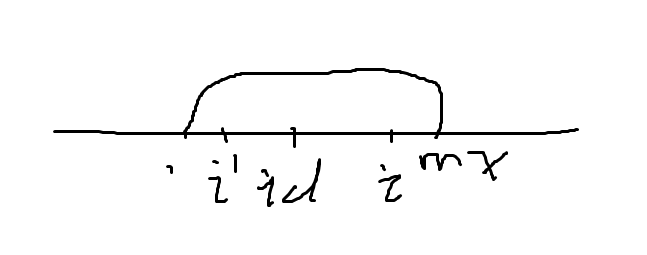
如上图所示i'代表i在id的对应左侧对应位置,如果以i为中心的回文串的边界不超过以id为中心的回文串的范围的话那么p[i] == p[i'],如果超过的话p[i] == 2*id-i,接下来在以为以为扩张p[i]。
由于每次扩张都会导致mx变大,而mx最大不会超过strlen(str2),所以时间复杂度为 。
#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
const int maxa = 111111*2;
int p[maxa*2];
#define max(a,b) a>b?a:b;
#define min(a,b) a<b?a:b;
int rebuild(int n, char* a, char* str){
for(int i = 0 ;i < n; i++){
a[i*2+1] = '#';
a[i*2+2] = str[i];
}
a[2*n+1] = '#';
a[2*n+2] = 0;
a[0] = '$';
return 2*n+2;
}
int manachar(int n, char* a){
int mx = 0, id = 0;
int ans = 0;
// printf("%s\n", a);
for(int i = 0; i < n; i++){
if(mx > p[i]){
int i2 = 2*id - i;
p[i] = min(mx - i, p[i2]);
}else p[i] = 0;
while(a[i-p[i]-1] == a[i+p[i]+1]){
p[i]++;
}
ans = max(ans, p[i]);
if(p[i] +i > mx){
id = i;
mx = p[i]+i;
}
}
return ans;
}
char str[maxa*2];
char a[maxa*2];
int main(){
while(scanf("%s", &str)!=EOF){
int n = strlen(str);
n = rebuild(n,a, str);
// printf("fuck");
printf("%d\n", manachar(n, a));
}
}
后缀数组
将字符串倒置接在原来字符串后,两个字符串之间用特殊字符分割,例如原串为abc,新串即为abc#cba。
我们将新串的前半部分称为str1,后半部分称为str2。
此时分两种情况,一种是求最长奇回文串,一种是求最长偶回文串。
- 求最长奇回文串。枚举以每个字符为中心时的奇回文长度,只要求出第
i个字符在str2中的位置,在求出两点的rank,然后求出两点rank之间的最小height,长度乘2减1就是以此点为中心的最长奇回文的长度。 - 求最长偶回文,求出某一节点在
str2中对应的位置的下一个节点,同(1)步骤求出的值*2即为以此点为中心右侧的偶回文的长度。
时间复杂度是 。
#include<iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
#define rep(i,n) for(int i = 0;i < n; i++)
using namespace std;
const int size = 222222,INF = 1<<30;
int rk[size],sa[size],height[size],w[size],wa[size],res[size];
void getSa (int len,int up) {
int *k = rk,*id = height,*r = res, *cnt = wa;
rep(i,up) cnt[i] = 0;
rep(i,len) cnt[k[i] = w[i]]++;
rep(i,up) cnt[i+1] += cnt[i];
for(int i = len - 1; i >= 0; i--) {
sa[--cnt[k[i]]] = i;
}
int d = 1,p = 0;
while(p < len){
for(int i = len - d; i < len; i++) id[p++] = i;
rep(i,len) if(sa[i] >= d) id[p++] = sa[i] - d;
rep(i,len) r[i] = k[id[i]];
rep(i,up) cnt[i] = 0;
rep(i,len) cnt[r[i]]++;
rep(i,up) cnt[i+1] += cnt[i];
for(int i = len - 1; i >= 0; i--) {
sa[--cnt[r[i]]] = id[i];
}
swap(k,r);
p = 0;
k[sa[0]] = p++;
rep(i,len-1) {
if(sa[i]+d < len && sa[i+1]+d <len &&r[sa[i]] == r[sa[i+1]]&& r[sa[i]+d] == r[sa[i+1]+d])
k[sa[i+1]] = p - 1;
else k[sa[i+1]] = p++;
}
if(p >= len) return ;
d *= 2,up = p, p = 0;
}
}
void getHeight(int len) {
rep(i,len) rk[sa[i]] = i;
height[0] = 0;
for(int i = 0,p = 0; i < len - 1; i++) {
int j = sa[rk[i]-1];
while(i+p < len&& j+p < len&& w[i+p] == w[j+p]) {
p++;
}
height[rk[i]] = p;
p = max(0,p - 1);
}
}
int getSuffix(char s[]) {
int len = strlen(s),up = 0;
for(int i = 0; i < len; i++) {
w[i] = s[i];
up = max(up,w[i]);
}
w[len++] = 0;
getSa(len,up+1);
getHeight(len);
return len;
}const int maxa = 222222;
char str[maxa];
int rmp[maxa][32];
int log(int n){
int cnt = 0;
while(n){
cnt ++;
n /= 2;
}
return cnt - 1;
}
int RMQ(int n){
for(int i = 0;i < n; i++){
rmp[i][0] = height[i];
}
int l = log(n);
for(int i = 1; i < l; i++){
for(int j = 0; j+(1<<(i-1)) < n; j++){
rmp[j][i] = min(rmp[j][i-1], rmp[j+(1<<(i-1))][i-1]);
}
}
}
int r1r2(int a, int b){
int j = log(b-a+1);
return min(rmp[a][j], rmp[b-(1<<j)+1][j]);
}
int main(){
while(scanf("%s", str)!=EOF){
int l = strlen(str);
str[l] = '#';
for(int i = 0; i < l; i++){
str[l+1+i] = str[l-1-i];
}
str[2*l+1] = 0;
//printf("%s\n", str);
getSuffix(str);
int n = strlen(str);
RMQ(n);
int ans = 0;
for(int i= 0; str[i] != '#'; i++){
int i1 = 2*l-i;
//printf("%d == i %d == i1\n", i, i1);
// printf("%d %d\n", rk[i], rk[i1]);
int a = rk[i], b = rk[i1];
// printf("%d ", 2*r1r2(min(a, b) + 1, max(a, b))-1);
ans = max(ans, 2*r1r2(min(a, b) + 1, max(a, b))-1);
i1++;
a = rk[i], b = rk[i1];
ans = max(ans, 2*r1r2(min(a, b) + 1, max(a, b)));
// printf("%d\n", 2*r1r2(min(a, b) + 1, max(a, b)));
}
printf("%d\n", ans);
}
}