强连通分量

有向图强连通分量：在有向图中有一些点，这些点中如果能从A到B，那么一定从B能到达A，这些点组成的点数最多的子图是原图的一个强连通分量。运用场合：有向图、有两两可达这种条件、往往通过把每个强连通分量缩点把原图化简成一棵树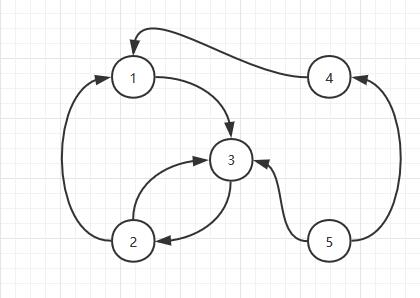

如图：

1,2,3号点构成了一个强连通分量，它们可以互相到达
4号点自己构成了一个强连通分量，5号点自己构成了一个强连通分量
所以图中一共有3个强连通分量
sccno[1] = 1 sccno[2] = 1 sccno[3] = 1 sccno[4] = 2 sccno[3] = 3
sccno[i]代表第i个点所在的强连通分量的编号

模板代码：

void dfs(int u) { //从u点开始找一个强连通分量
    pre[u] = lowlink[u] = ++dfs_clock;
    S.push(u);
    for (int i = 0; i < (int)G[u].size(); i++) {
        int v = G[u][i];
        if (!pre[v]) {
            dfs(v);
            if (lowlink[u] > lowlink[v]) lowlink[u] = lowlink[v];
        } else if (!sccno[v]) {
            if (lowlink[u] > pre[v]) lowlink[u] = pre[v];
        }
    }
    if (lowlink[u] == pre[u]) {
        scc_cnt++;
        for(;;) {
            int x = S.top(); S.pop();
            sccno[x] = scc_cnt;
            if (x == u) break;
        }
    }
}
void find_scc(int n) { //n是点的总数，点的范围1-n
    dfs_clock = scc_cnt = 0;
    MEM(sccno); MEM(pre); MEM(ans);
    for (int i = 1; i <= n; i++) {
        if (!pre[i]) dfs(i);
    }
}

POJ 3180 The Cow Prom

有N头奶牛，和M个绳索。每个绳索从一头奶牛处发出，射向另一头奶牛。现在奶牛们想要跳舞，如果沿着射向它的绳索往回找，找到另一头牛，并如此找下去，最后能找到自己发出的绳索，那么这头奶牛就跳舞成功了，并且在寻找过程中，串起来的这些奶牛属于同一个集合。问最后这M个绳索连出了几个集合？
先明确什么是同一个集合，A->B->C->D->E->A这样A,B,C,D,E就是同一个集合，如果还有C->F->C，那么F也属于上面那个集合，所以这题就是求点数大于2的强连通分量的个数。
大白书的模板（Tarjan）中用了一个sccno[]数组，sccno[i]记录第i个点所属的强连通分量号然后我们只需要用一个cnt[]数组，记录每个块中点的个数，如果cnt[i] > 1，说明第i个块是符合条件的，答案数目加1，最后输出答案数。

#include <cstdio>
#include <cstring>
#include <stack>
#include <vector>
using namespace std;

#define MEM(a) memset(a, 0, sizeof(a))
const int maxv = 21000;
vector<int>G[maxv];
int pre[maxv], lowlink[maxv], sccno[maxv], ans[maxv], dfs_clock, scc_cnt;
stack<int>S;

void dfs(int u) {
    pre[u] = lowlink[u] = ++dfs_clock;
    S.push(u);
    for (int i = 0; i < (int)G[u].size(); i++) {
        int v = G[u][i];
        if (!pre[v]) {
            dfs(v);
            if (lowlink[u] > lowlink[v]) lowlink[u] = lowlink[v];
        } else if (!sccno[v]) {
            if (lowlink[u] > pre[v]) lowlink[u] = pre[v];
        }
    }
    if (lowlink[u] == pre[u]) {
        scc_cnt++;
        for(;;) {
            int x = S.top(); S.pop();
            sccno[x] = scc_cnt;
            if (x == u) break;
        }
    }
}
void find_scc(int n) {
    dfs_clock = scc_cnt = 0;
    MEM(sccno); MEM(pre); MEM(ans);
    for (int i = 1; i <= n; i++) {
        if (!pre[i]) dfs(i);
    }
}

int main() {
    int n, m, u, v;
    while (scanf("%d%d", &n, &m) != EOF) {
        for (int i = 1; i <= n; i++) G[i].clear();
        for (int i = 0; i < m; i++) {
            scanf("%d%d", &u, &v);
            G[u].push_back(v);
        }
        find_scc(n);
        for (int u = 1; u <= n; u++) {
            ans[sccno[u]]++;
        }
        int cnt = 0;
        for (int i = 1; i <= scc_cnt; i++)
            if (ans[i] > 1) cnt++;
        printf("%d\n", cnt);
    }
    return 0;
}

HDU 3816 The King’s Problem

有一个n个点m条边的有向图，把这个图分成几个区域，使得每个区域中的任意两点u, v要么u能到v，要么v能到u，求最少要分成几个区域

缩点得到有向的树，即求这棵树的最少路径覆盖(点数 – 二分图的最大匹配)

#include <cstdio>
#include <cstring>
#include <stack>
#include <vector>
using namespace std;

#define MEM(a) memset(a, 0, sizeof(a))
const int maxv = 15100;
vector<int>G[maxv], H[maxv];
int pre[maxv], lowlink[maxv], sccno[maxv], left[maxv], dfs_clock, scc_cnt;
bool vis[maxv];
stack<int>S;

void dfs(int u) {
    pre[u] = lowlink[u] = ++dfs_clock;
    S.push(u);
    for (int i = 0; i < (int)G[u].size(); i++) {
        int v = G[u][i];
        if (!pre[v]) {
            dfs(v);
            if (lowlink[u] > lowlink[v]) lowlink[u] = lowlink[v];
        } else if (!sccno[v]) {
            if (lowlink[u] > pre[v]) lowlink[u] = pre[v];
        }
    }
    if (lowlink[u] == pre[u]) {
        scc_cnt++;
        for(;;) {
            int x = S.top(); S.pop();
            sccno[x] = scc_cnt;
            if (x == u) break;
        }
    }
}

void find_scc(int n) {
    dfs_clock = scc_cnt = 0;
    MEM(sccno); MEM(pre);
    for (int i = 1; i <= n; i++) {
        if (!pre[i]) dfs(i);
    }
}

bool match(int u) {
    for (int i = 0; i <(int)H[u].size(); i++) {
        int v = H[u][i];
        if (!vis[v]) {
            vis[v] = 1;
            if (left[v] == -1 || match(left[v])) {
                left[v] = u;
                return true;
            }
        }
    }
    return false;
}

int main() {
    int n, m, u, v, t;
    scanf("%d", &t);
    while (t--) {
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++) {
            G[i].clear();
            H[i].clear();
        }
        for (int i = 0; i < m; i++) {
            scanf("%d%d", &u, &v);
            G[u].push_back(v);
        }
        find_scc(n);
        for (int u = 1; u <= n; u++) {
            for (int i = 0; i < (int)G[u].size(); i++) {
                int v = G[u][i];
                if (sccno[u] != sccno[v])
                    H[sccno[u]].push_back(sccno[v]);
            }
        }
        int sum = 0;
        memset(left, -1, sizeof(left));
        for (int i = 1; i <= scc_cnt; i++) {
            MEM(vis);
            if (match(i)) sum++;
        }
        printf("%d\n", scc_cnt-sum);
    }
    return 0;
}

强连通分量