双连通分量

无向图中的双连通分量有两种：点双连通分量和边的连联通分量，如果去掉任意一个点之后，这个图还是连通的，就说这个图是点双连通的。如果去掉任意一条边之后这个图还是连通的，就说明这个图是边双连通的。
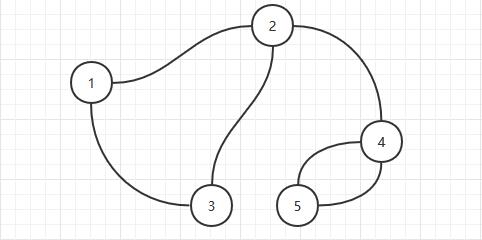
如图：

• 1，2，3构成了一个边双连通分量，切断1，2，3中的任意一条边它们还连着
• 4，5构成了一个边双连通分量，切断4，5中的任意一条边它们还连着
• 1，2，3构成了一个点双连通分量，去掉1，2，3中的任意一个点它们还连着

模板代码

void dfs(int u, int fa) {
    low[u] = pre[u] = ++dfs_clock;
    stakk[top++] = u;
    for (int i = 0; i < (int)G[u].size(); i++) {
        int v = G[u][i];

        if (!pre[v]) {
            dfs(v, u);
            low[u] = min(low[u], low[v]);
        } else if (pre[v] < pre[u] && v != fa) {
            low[u] = min(low[u], pre[v]);
        }
    }
    if (pre[u] == low[u]) {
        while (top > 0 && stakk[top] != u) {
            low[stakk[--top]] = low[u];
        }
    }
}

void find_bcc(int n) {
    MEM(pre); MEM(low);MEM(deg);
    dfs_clock = top = 0;
    for (int i = 1; i <= n; i++)
        if (!pre[i]) dfs(i, -1);
}

POJ 3352 Road Construction

给出一个没有重边的无向图，求至少加入几条边使整个图成为一个边双连通分量

把图中所有的边双连通分量缩成一个点，原图就缩成了一棵树，要加的边数就是(所有度为1的点的个数 + 1)/2

#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;

#define MEM(a) memset(a, 0, sizeof(a))
#define pb push_back
const int maxv = 1010;

int pre[maxv], low[maxv], deg[maxv], stakk[maxv];
int dfs_clock, top;
vector<int> G[maxv];

void dfs(int u, int fa) {
    low[u] = pre[u] = ++dfs_clock;
    stakk[top++] = u;
    for (int i = 0; i < (int)G[u].size(); i++) {
        int v = G[u][i];

        if (!pre[v]) {
            dfs(v, u);
            low[u] = min(low[u], low[v]);
        } else if (pre[v] < pre[u] && v != fa) {
            low[u] = min(low[u], pre[v]);
        }
    }
    if (pre[u] == low[u]) {
        while (top > 0 && stakk[top] != u) {
            low[stakk[--top]] = low[u];
        }
    }
}

void find_bcc(int n) {
    MEM(pre); MEM(low);MEM(deg);
    dfs_clock = top = 0;
    for (int i = 1; i <= n; i++)
        if (!pre[i]) dfs(i, -1);
}
int main() {
    int n, m, u, v;
    while (scanf("%d%d", &n, &m) != EOF) {
        for (int i = 1; i <= n; i++) G[i].clear();

        for (int i = 0; i < m; i++) {
            scanf("%d%d", &u, &v);
            G[u].pb(v); G[v].pb(u);
        }
        find_bcc(n);
        int ans = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j < (int)G[i].size(); j++) {
                if (low[i] != low[G[i][j]]) {
                    deg[low[i]]++;
                    deg[low[G[i][j]]]++;
                }
            }
        }
        for (int i = 1; i <= n; i++)
            if (deg[i]/2 == 1) ans++;
        printf("%d\n", (ans+1)/2);
    }        
    return 0;
}

LA 3523 Knights of the Round Table

亚瑟王要给一些骑士开会，但是这些骑士中有一些相互憎恨，所以他们不能在圆桌中相邻，为了投票不出现支持的人数和反对的人数相等的情况，每个圆桌中的骑士的个数必须为奇数个，问有多少个骑士一定不能参加任何一个会议。

因为可能要开好几桌会议，所以要求出图中所有的连通分量，又因为要求骑士的个数为奇数个，所以求每个联通分量中不在奇圈上的点的个数的和

#include <cstdio>
#include <stack>
#include <cstring>
#include <vector>
using namespace std;

#define MEM(a) memset(a, 0, sizeof(a))
const int maxv = 1100;
const int maxe = maxv*maxv;

vector<int>G[maxv], bcc[maxv];
int dfs_clock, bcc_cnt, pre[maxv], low[maxv], bccno[maxv];
int color[maxv], odd[maxv], mapp[maxv][maxv];
struct Edge{
    int u, v;
    Edge(){}
    Edge(int a, int b) {
        u = a;
        v = b;
    }
};
stack<Edge> S;

bool bipartite (int u, int b) {
    for (int i = 0; i < (int)G[u].size(); i++) {
        int v = G[u][i];
        if (bccno[v] != b) continue;
        if (color[v] == color[u]) return false;
        if (!color[v]) {
            color[v] = 3 - color[u];
            if (!bipartite(v, b)) return false;
        }
    }
    return true;
}

void tarjan(int u, int fa) {
    pre[u] = low[u] = ++dfs_clock;
    for (int i = 0; i < (int)G[u].size(); i++) {
        int v = G[u][i];
        if (!pre[v]) {
            S.push(Edge(u, v));
            tarjan(v, u);
            low[u] = min(pre[v], low[u]);
            if (low[v] >= pre[u]) {
                bcc_cnt++;
                bcc[bcc_cnt].clear();
                for(;;) {
                    Edge x = S.top(); S.pop();
                    if (bccno[x.u] != bcc_cnt) {
                        bcc[bcc_cnt].push_back(x.u);
                        bccno[x.u] = bcc_cnt;
                    }
                    if (bccno[x.v] != bcc_cnt) {
                        bcc[bcc_cnt].push_back(x.v);
                        bccno[x.v] = bcc_cnt;
                    }
                    if (x.u == u && x.v == v) break;
                }
            }
        }
        else if (pre[v] < pre[u] && v != fa) {
            S.push(Edge(u, v));
            low[u] = min(low[u], pre[v]);
        }
    }
}

void find_bcc(int n) {
    dfs_clock = bcc_cnt = 0;
    MEM(pre); MEM(low);
    for (int i = 1; i <= n; i++)
        if (!pre[i]) tarjan(i, -1);
}
int main() {
    int n, m, u, v;
    while (scanf("%d%d", &n, &m) != EOF &&m && n) {
        MEM(mapp);
        for (int i = 1; i <= n; i++) G[i].clear();
        for (int i = 0; i < m; i++) {
            scanf("%d%d", &u, &v);
            mapp[u][v] = mapp[u][v] = 1;
        }
        for (int u = 1; u <= n; u++) {
            for (int v = u+1; v <= n; v++) {
                if (!mapp[u][v]) {
                    G[u].push_back(v);
                    G[v].push_back(u);
                }
            }
        }
        find_bcc(n);

        MEM(odd);
        for (int i = 1; i <= bcc_cnt; i++) { //对于图中的每个点双连通分量
            MEM(color);
            for (int j = 0; j < (int)bcc[i].size(); j++) bccno[bcc[i][j]] = i;
            //给双连通分量里的每个点标号
            int u = bcc[i][0]; // 找到代表的点
            color[u] = 1;
            if (!bipartite(u, i))   //判断如果这个双连通分量不是二分图，那么这个连通分量里的点都合格
                for (int j = 0; j < (int)bcc[i].size(); j++) odd[bcc[i][j]] = 1;
        }
        int ans = n;
        for (int i = 1; i <= n; i++) if (odd[i]) ans--;
        printf("%d\n", ans);
    }
    return 0;
}