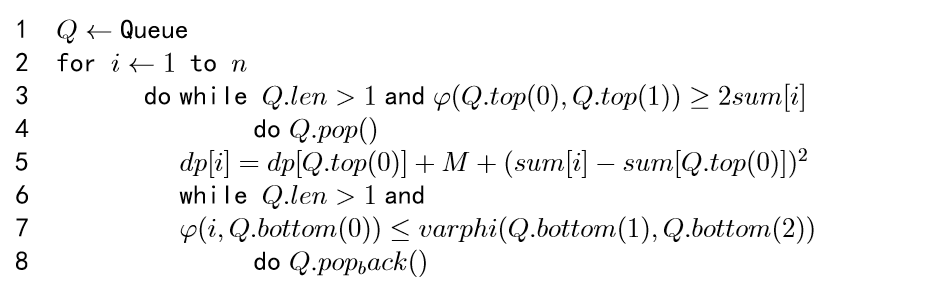• 动态规划的优化
  • 前言
  • 时间复杂度优化
    • 改进状态表示
      • 例题
        • 题目大意
        • 最初的分析
        • 改进
    • 决策单调性 · 四边形不等式
      • 例题1
        • 最初的分析
        • 改进
      • 例题2 Post Office
    • 决策单调性 · 斜率优化
      • 例题 Print Article
        • 改进

动态规划的优化

前言

动态规划在解决问题的时候，利用的是保存中间状态来减少重复的计算次数的方法来减少时间消耗的。可是在很多问题中，动态规划的时间效率，或者空间复杂度都不能满足我们的要求（超出我们的限制），这时候就要考虑对算法进行时间或者空间上的优化。

时间复杂度优化

动态规划问题总的来说还是对枚举的优化，即保存中间状态来减少计算次数的方法。那么就可以大概的认为，一个动态规划问题的时间复杂度应该是：时间复杂度 = 状态总数 * 状态转移总数 * 状态转移时间。我们只要减少任意一个部分，都可以达到加速动态规划的方式。

改进状态表示

即通过改变状态的表示方式来减少状态总数的方法。这种方法通常是一开始想出来的状态表示方法并不够好，还有我们没有发现的关系或者条件。在这种时间，我们可以对状态的表示方法进行优化，用一种更优的表示方法。这样在转义数量和转移时间不变的情况下，时间复杂度就已经被减小了。

例题

题目大意

把 $n$ 个数字，分成 $m$ 组。每组的和不能大于 $t$。分组必须是有序的，并且保证所有的数字都是小于 $t$ 的。求最多能把多少数字划入分组里。

最初的分析

这里我们用w[i]来表示第i个数的值，用dp来表示我们的结果数组。那么我们可以显然的得到一个状态表示：$dp[i][j][k]=x$，来表示前 $i$ 个数字，分成 $j$ 组，还多了 $k$ 的时候，最多有多少个数字被划入了分组中。
可以显然的得到，这里整个问题的最优解应该是 $dp[n][m][0]$。通过状态的表示，我们可以得到状态转移方程： $$dp[i][j][k] \left\{ \begin{array}{ll} max(dp[i-1][j][k-w[i]],dp[i-1][j][k]) & k\leq w[i],i \geq 1\\ max(dp[i-1][j-1][t-w[i]],dp[i-1][j][k]) & k < w[i], i \geq 1\\ 0 & 0\leq k < t \end{array} \right.$$ 这样时间复杂度应该是 $O(nmt)$ 的。因为总状态数是 $O(nmt)$，每次状态转移的状态数为 $O(1)$，总时间为 $O(nmt)$。

改进

改进后的状态表示：$dp[i][j]=(x,y)$，表示在前 $i$ 中选 $j$ 个所需要的最少的分组为 $x$ 另外还需要 $y$。
通过状态的表示，我们可以得到状态转移方程： $dp[i][j] = min(dp[i-1][j], g[i-1][j-1]+w[i])$ 其中，$(x, y) + w[i] = (x',y')$计算方法为： $$\begin{array}{ll} x'=x,y'=y+w[i]&w[i]\leq t-y\\ x'=x+1,y'=w[i]&w[i]>t-y \end{array}$$ 时间复杂度从$O(nmt)$，降到了$O(n^2)$。这里空间复杂度也同时降低了。

决策单调性 · 四边形不等式

例题1

在一个操场上摆放着一排$n(n\leq20)$堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的2堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。求出将 $n$ 堆石子合并成一堆的最小得分和最大得分以及相应的合并方案。

最初的分析

这里最大得分和最小得分的思路是一样的。这里只取最小得分来说明问题。

令每堆石子的个数为：$d[1\ldots n]$。我们可以得到最基础的状态表示：$m[i][j]$ 来表示合并第 $i$ 个到第 $j$ 个石子堆所获得的最小得分。得到了状态转移方程和边界条件： $$\begin{array}{ll} m[i][j]=0 & i=j m[i][j]=min_{i<k\leq j}\{m[i][k-1]+m[k][j]+\sum_{l=i}^{j}d[l]\} \end{array}$$ 并且把最优解保存在 $s[i][j]$ 中。（这里的 $\sum_{l=i}^{j}d[l]$ 部分可以用 $O(n^2)$ 的时间复杂度预处理，这样直接引用就好了。）
总的时间复杂度：$O(n^3)$

改进

• 定理1 当函数 $w(i,j)$ 满足 $w(i,j)+w(i',j')\leq w(i',j)+w(i,j'),i\leq i'\leq j\leq j'$ 时，则称函数 $w$ 满足四边形不等式。
• 定理2 当函数 $w(i,j)$ 满足 $w(i',j)\leq w(i,j'),i\leq i'\leq j\leq j'$ 时，则称函数 $w$ 关于区间包含关系单。

在这个问题中。另 $w(i,j)=\sum_{l=i}^{j}d[l]$，可以显然得到 $w(i,j)$ 是满足四边形不等式的，同时也满足区间包含关系单调。根据 $m$ 的递推式： $$\begin{equation} m[i][j]=min_{j<k\leq j}\{m[i][k-1]+m[k][j]\}+w(i,j) \end{equation}$$ 对于满足四边形不等式的函数 $w$ 这里我们要证明，会使 $m$ 也满足四边形不等式。

这里当 $i=i'$ 或者 $j=j'$ 的时候，不等式显然成立。当 $i<i'=j<j'$ 时。原式可以简化为： $m[i][j]+m[j,j']\leq m[i][j']$的形式。设这时候取到最优值时的 $l=k$。这里又分为两种情况，$k\leq j$ 和 $k>j$。只讨论前一种情况，因为后一种和前一种是镜像的。 $$\begin{array}{rll} m[i][j]+m[j][j'] & = & w(i,j)+m[i][k-1]+m[k][j]+m[j][j']\\ & \leq & w(i,j')+m[i][k-1]+m[k][j]+m[j][j']\\ & \leq & w(i,j')+m[i][k-1]+m[k][j']\\ & = & m[i][j'] \end{array}$$ 当 $i<i'<j<j'$ 的时候，设 $l=y$ 时 $m[i'][j']$ 取最优值，同 $z$ 对于 $m[i][j]$。 这里同样要分情况 $z\leq y$ 和 $z>y$。还是只讨论前一种，后一种是相似的。 $$\begin{array}{rll} m[i][j]+m[i'][j'] & = & w(i,j)+m[i][z-1]+m[z][j]+w(i',j')+m[i'][y-1]+m[y][j]\\ & \leq & w(i,j')+w(i',j)+m[i'][y-1]+m[i][z-1]+m[z][j]+m[y][j']\\ & \leq & w(i,j')+w(i',j)+m[i'][y-1]+m[i][z-1]+m[y][j]+m[z][j']\\ & = & m[i][j']+m[i'][j] \end{array}$$ 综上，$m[i][j]$ 满足四边形不等式。其决策满足单调性，即：记 $s[i][j]$ 为 $m[i][j]$ 取最优值时的决策，有： $$\begin{equation} s[i][j]\leq s[i][j+1]\leq s[i+1][j+1], i \leq j \end{equation}$$

这里要证明一下上面的那个式子成立。 令：$m_{k}[i][j]=m[i][k-1]+m[k][j]+w(i,j)$，要证明 $s[i][j]\leq s[i][j+1]$，也就是证明对于所有的 $i<k\leq k'\leq j$ 且 $m_{k'}[i][j] \leq m_{k}[i][j]$，有： $$m_{k'}[i][j+1]\leq m_{k}[i][j+1]$$ 这里有一个更强的不等式， $$m_{k}[i][j]-m_{k'}[i][j]\leq m_{k}[i][j+1]-m_{k'}[i][j+1]$$ 即： $$m_{k}[i][j]+m_{k'}[i][j+1]\leq m_{k}[i][j+1]+m_{k'}[i][j]$$ 展开得到： $$m[k][j]+m[k'][j+1]\leq m[k'][j]+m[k][j+1]$$ 这恰好是 $k\leq k'\leq j\leq j+1$ 时的四边形不等式的形式。

所以，当$w$满足四边形不等式的时候，$s[i][j]$的取值满足单调性。

这样我们就可以改写我们的状态转移方程了，因为我们的决策的范围已经被缩小了。 $$\begin{array}{ll} m[i][j]=0 & i=j\\ m[i][j]=min_{s[i][j-1]\leq k\leq s[i+1][j]}\{m[i][k-1]+m[k][j]\}+w(i,j) \end{array}$$ 时间复杂度：$O(n^2)$。

例题2 Post Office

这题简单的DP是可以通过的。不过如果把数据范围扩大了，就可以用上面说的四边形不等式优化去优化。略去证明，这道题直接给出伪代码：

决策单调性 · 斜率优化

在说斜率优化之前，要先说一下另一个优化方式。当我们发现一个dp的状态转移方程形如这样的形式的时候， $$dp(i) = f(j) + g(i)$$ 也就是说，一个 $i$ 的结果可以化成一个于 $i$ 无关的函数的和另一个只与 $i$ 有关的形式的时候。我们可以对前面的和 $i$ 无关的部分放在一个优先队列里，这样可以把本来 $O(n)$ 的查找代价，变成 $\log n$ 的。

但是这终归是一个非常理想的方程啊，实际问题中这种良心满满的题目基本是没有的。所以一种把条件放的稍微弱一点的优化方式，就是斜率优化。也是通过结果和决策的关系，发现决策有事满足一些神奇的数量关系的。

例题 Print Article

状态表示：$dp[i]$来表示，从第一个到第 $i$ 个输出的最少花费。
很容易得到状态转移方程： $$\begin{equation} dp[i] = min_{0 \leq j < i}{dp[j]+M+sum[j+1 \ldots i]^2} \end{equation}$$ 这个的时间复杂度可以很显然的计算出来，是 $O(n^2)$ 的。显然，我们是不能接受这种时间复杂度的，因为数据范围非常大。

改进

这里，我们先假设，上式中的 $j$ 取值为 $k_1$ 的时候，比取 $k_2$ 的时候更优。也就是： $$dp[k_1]+sum[k_1+1 \ldots i]^2 < dp[k_2] + sum[k_2+1 \dots i]^2$$ 其中，这里我们可以预处理得到一个 $sum$ 数组。那么：$sum[k_1+1 \ldots i] = sum[i]-sum[k_1]$，同理对于 $k_2$ 的部分。移项得到： $$\begin{equation} (dp[k_1]+sum[k_1]^2)-(dp[k_2]+sum[k_2]^2) < 2*sum[i] * (sum[k_1]-sum[k_2]) \end{equation}$$ 其中所有的项都是我们已经计算好得到了的。我们 $f(i)=dp[i]+sum[i]^2$，$g(i)=sum[i]$。上可以化成： $$\begin{equation} \frac{f(k_1)-f(k_2)}{g(k_1)-g(k_2)} < 2 \times sum[i] \end{equation}$$ 如果以 $f(i)$ 为Y轴，以 $g(i)$ 为X轴，那么上面个式子就是两点之间的斜率。并把这个值表示为：$\varphi(k_1,k_2)$。

然后我们来说明他们之间的单调性关系。即，若有 $\varphi(i,j)<\varphi(j,k)$，那么 $j$ 这个点一定是不可能是最优解的。

证明如下：
当 $\varphi(i,j)<2sum[x]$，也就是说明 $i$ 比 $j$ 更优，排除 $j$ 点。 当 $\varphi(i,j)\geq 2sum[x]$，说明 $j$ 比 $i$ 更优，但是此时 $\varphi(j,k) > \varphi(i,j) \geq 2sum[x]$，也就是 $k$ 比 $j$ 更优，也就是 $j$ 是没用的。
也就是说，对于一个 $k<j<i$ 的状况下，如果有：$\varphi(i,j)<\varphi(j,k)$ 的话，那么 $j$ 是可以删去的。也就是说，最终留下的所有有效点都满 $\varphi(i,j)>\varphi(j,k),k<j<i$ ，也就是说整个图形呈现一个上凸的形状。如何维护图形的上凸可以用凸包的算法去解决。
唯一的就是在求解结果的时候，要从队列的头部一直找到第一个满足 $\varphi(k_1,k_2)<2sum[i]$ 的值。

伪代码：