a*算法
算法简述
我们尝试解决的问题是:对象从起点出发,移动到终点。路径搜索的目标:找到一条路径,避免障碍物,敌人等,并且把代价(时间,距离,金钱等)最小化。
移动一个简单的对象看起来是容易的,但是路径搜索可能是比较复杂的。考虑下面情况:
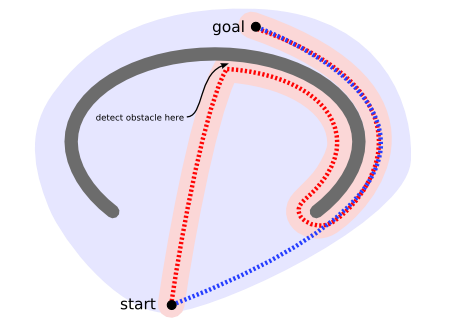
初始节点 start ,目标节点 goal,灰色部分表示障碍物,第一种情况,我们只考虑怎样能使得我们目前所花费的是最少,搜索到的路径会如图中粉色部分所示。同时它所搜索的范围是淡粉色部分,另一种情况,我们考虑所要走的下一个节点,是下一步的所有可能中,距离goal的花费是最少的。我们所得到的路径时蓝色部分,搜索的范围是淡蓝色部分。
注意以上是两种搜索方法,两种算法所考虑的代价是不同的,这就直接影响了我们的搜索代价。并且从图中两种方法的搜索路径和扫描范围可以看出,第1种情况搜索代价少,但是所花费的最终结果并不是最优的。想法第2种情况最终花费虽然是最优的,但是搜索代价非常大。

dijkstra’s algorithm and best-first-search
在介绍a*之前,我们先来看这两种算法。 dijkstra算法从物体所在的初始节点开始,在访问途中的节点时候,它迭代检查的是当前节点的临近节点,并且把和该节点最近的尚未访问的节点加入待访问队列,直到到达目标节点。dijkstra算法保证能在一般简单且边是非负的图中,找到一条从初始节点到目标节点的最短路径。下图中粉色代表初始节点,紫色代表目标节点,蓝色表示扫描过的区域。颜色越浅表示离初始节点越远。
最佳优先搜算法与dijkstra算法的不同之处就在于其是采用启发式函数。它能够评估任意节点到目标节点的代价。与选择距离初始节点最近的算法不同。它选择离目标节点的估计代价最小的节点。最佳优算法不能保证一定会找到一条路径。但是相同情况下它会比dijkstra算法快很多。图中黄色渐变部分表示最佳优先搜索算法所扫描过的部分,其颜色越深表示离目的节点越近。
那么现在来让我们来看一个相对较复杂的图。下图较上图中多加了一个u型的障碍物。


此障碍物不可穿越。
上图中虚线表示用dijstra算法所找的的路径,同样淡蓝色表示扫码过的路径。由此可看出dijkstra确实可以确保找的一条路径,但是扫描的代价很大。
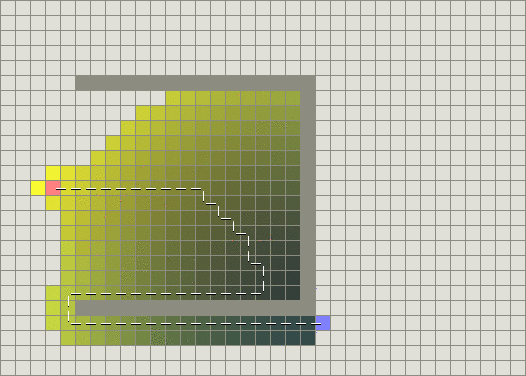
上图中采用最佳优先搜索算法,可以看出虽然最佳优先搜索算法虽在扫描小部分的情况下可以找的一条路径,但是并不是最优的。
问题就在于最佳优先搜索算法是基于贪心的。它是试图尽可能的向目标节点移动,尽管这条路并不是很正确。它仅仅考虑了到达目标节点的代价,而并未考虑到目前为止已花费的代价。
基于两者的缺点和优点,1968年发明了a*算法。其把启发式算法和常规的算法结合在了一起,但是与单纯的启发式算法不同。在村庄最短路径的情况下,a*保证一定能找到最短路径。
主要运用场合及思路
a*算法;a*(a-star)算法是一种静态路网中求解最短路径最有效的直接搜索方法。估价值与实际值越接近,估价函数取得就越好。

a*采用启发式函数,在简单情况下它和最佳优先算法一样快。
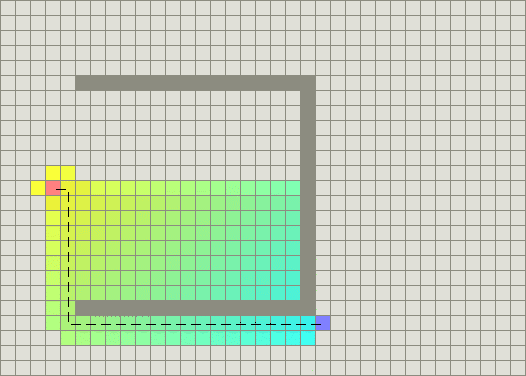
在有障碍物时,a*和dijkstra算法一样可以找的一条最优路径。
a*算法把dijkstra算法和最佳优先算法相结合,g(n)表示从初始节点到当前节点n的代价,h(n)表示从当前节点n到目标节点的启发式估计代价。a*权衡这两者,每次进行主循环时,它检测f(n)中最小的节点n,其中f(n) = g(n) + h(n)。
循环时,它检测f(n)中最小的节点n,其中f(n) = g(n) + h(n)。
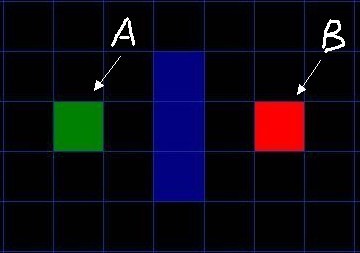
首先,如图所示简易地图, 其中绿色方块的是起点 (用 a 表示), 中间蓝色的是障碍物, 红色的方块 (用 b 表示) 是目的地.
假设我们当前求的是最短路,那g(n)就表示从起点到其的最短代价,而h(n)就表示从当前节点到目标节点的估计代价。
具体寻路步骤:
- 从起点开始,把它作为一个待处理的节点,存入待处理队列。这个队列就是一个等待处理的队列。
- 取起点a可以到达的所有未访问过的邻居节点,将他们放入队列,并设置他们的父亲节点为a,
- 在待处理队列中删除起点a,节点并标记已访问过,不需要再次访问。

图中浅绿色描边的方块表示已经加入待处理队列,等待处理. 荧光标记的起点 a 表示已经放入 已访问队列, 它不需要再执处理。
从待处理队列中找出相对最优的节点, 那么什么是最优呢,最优世通过公式f(n) = g(n) + h(n) 来计算的.(g(n)表示从初始节点到当前节点n的代价,h(n)表示从当前节点n到目标节点的启发式估计代价)。
我们假设横向移动一个格子的耗费为10, 为了便于计算, 沿斜方向移动一个格子耗费是14. 图中方块的左上角数字表示 f(n), 左下角表示 gg(n) 右下角表示 h(n) 看看是否跟你心里想的结果一样?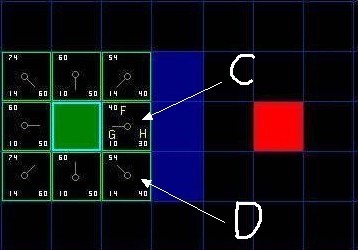
- 从待处理队列中选择 f(n) 值最低的方格 ,本图当前步骤是c (绿色起始方块 a 右边的方块), 把其从待处理队列中删除,并放入到已访问队列中。
- 检查其所有可到达的未访问过的队列中的节点,如果其不在待处理队列中,则把他们加入待处理队列,否则转到步骤6,计算这些节点的f(n), g(n), h(n)。并设置他们的父亲节点为c。
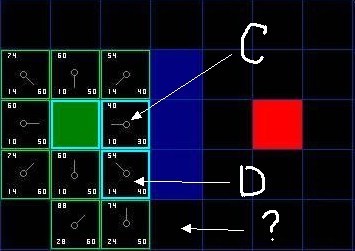
- 对于已经存在待处理队列中的节点(如d),检查通过当前节点(即本例c)到达它的话,g(n)的值是否更优一些,如果是,那么就把其父亲节点标记成当前节点(本例中c)然后从新计算其 f(n), g(n), 不过h(n) 不需要计算(其实对于本例求最短路中,每个及诶单的h(n)是不变的)。如果经过当前节点得到的代价反而不是较优的话,我们什么也不用做。
如上图, 我们选中了 c 因为它的 f(n) 值最小, 我们把它从待处理对了中删除, 并把它加入 已访问队列. 它右边上下三个都是墙, 所以不考虑它们. 它左边是起始方块, 已访问过了, 也不考虑. 所以它周围的候选方块就只剩下 4 个. 让我们来看看 c 下面的那个格子, 它目前的 g 是14, 如果通过 c 到达它的话, g将会是 10 + 10, 这比 14 要大, 因此我们什么也不做.
然后我们继续从待处理队列中找出 f 值最小的(即重复4,5,6步骤), 但我们发现 待处理队列中,处于c 上面的和下面的同时为 54, 这时怎么办呢? 这时随便取哪一个都行, 比如我们选择了 c 下面的那个方块 d.
d 右边以及右上方的都是墙, 所以不考虑, 但为什么右下角的没有被加进 待处理队列呢? 因为如果 c 下面的那块也不可以走, 想要到达 c 右下角的方块就需要从 "方块的角" 走了, 在程序中设置是否允许这样走. (图中的示例不允许这样走)
我们一直重复这些步骤知道我们访问到目标节点为止。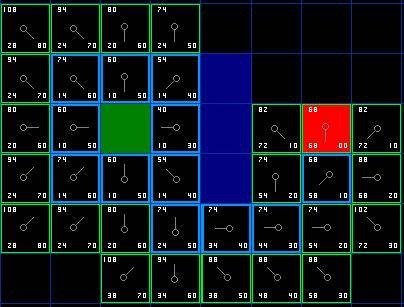
- 起时我们得到路径的过程是一个回溯的过程,因为之前已经记录了各个节点的父亲节点。 伪代码:
do
{
fleast=heap.pop(); //从queue取fcost最小的元素
current=fleast; //取出的元素作为当前节点
least.flag = 1 //1:visited 0:not on queue not visited
for(int i=current.x-1;i<current.x+1;i++) //考察当前节点的所有相邻节点
for(int j=current.y-1;j<current.y+1;j++)
{
if(map[i][j]!=unwalkable||!onclose(node(i,j))) //相邻节点可通并且没有考察过
{
if(!onopen(node(i,j))) //相邻节点不在queue中
{
heap.add(node(i,j)); //加入queue
node(i,j).parent=current; //设置相邻节点的父节点为当前节点
node(i,j).calculate(f,g,h); //重新计算fcost,gcost,hcost
if(node(i,j)==dest) //如果加入的节点是目标点则找到路径
path=find;
}
else
{
temp.gcost=parent.gcost+addcost; //相邻节点已经在queue中
node(i,j).hcost=10*(abs(i-parent.x)+abs(j-parent.y));
node(i,j).fcost=node(i,j).gcost+node(i,j).hcost;
if(tempgcost<node(i,j).gcost)
node(i,j).parent=current;
node(i,j).recaculate(f,g,h); //重新计算fcost,gcost,hcost
}
}
}while(!hp.isempty()) //如果堆空则没有找到路径
if(path==find)
outpath; //输出路径
else
cout<<"path not find;!"<<endl;
模板代码
#define maxn 111111
#define inf 0x1f1f1f1f
int head[maxn], head1[maxn], ecnt1, ecnt2;
int dist[maxn];
bool vis[maxn];
int sta, end;
struct edge
{
int v, t, next;
edge(){}
edge( int _v, int _t)
{
v = _v;
t = _t;
}
}e[maxn], e1[maxn];
void init()
{
memset(head, -1, sizeof(head));
memset(head1, -1, sizeof(head1));
ecnt1 = ecnt2 = 0;
}
void addedge( int u, int v, int t)
{
e[ecnt1] = edge(v,t);
e[ecnt1].next = head[u];
head[u] = ecnt1++;
e1[ecnt2] = edge(u,t);
e1[ecnt2].next = head1[v];
head1[v] = ecnt2++;
}
struct point
{
int v, g;
point(){};
point(int _v, int _g)
{
v = _v;
g = _g;
}
bool operator <(const point &a) const
{
return dist[v] + g > dist[a.v] + a.g;
}
};
priority_queue<point> que;
int a_start( int k)
{
while(!que.empty()) que.pop();
point now, tem;
now = point(sta, 0);
que.push(now);
while(!que.empty())
{
now = que.top();
que.pop();
if(now.v == end)
{
if(k > 1)
k--;
else
return now.g;
}
for( int i = head[now.v]; i != -1; i = e[i].next)
{
que.push(point(e[i].v,e[i].t + now.g));
}
}
return -1;
}
POJ 2449
题目描述:给出一个图,一个起点个一个终点,求这两点间的第k短路。
思路及关键的:是可以走重复的路的,所以如果一张图中有一个环的话,无论求第几短路都是存在的。
对于a* ,估价函数 = 当前值+当前位置到终点的距离,即 f(p)=g(p)+h(p),每次扩展估价函数值中最小的一个。对于k短路来说,g(p)为当前从s到p所走的长度,h(p)为从p到 t 的最短路的长度,则f(p)的意义就是从s按照当前路径走到 p 后要走到终点 t 一共至少要走多远。也就是说我们每次的扩展都是有方向的扩展,这样就可以提高求解速度和降低扩展的状态数目。为了加速计算,h(p)需要从a*搜索之前进行预处理,只要将原图的所有边反向,再从终点 t 做一次单源最短路径就可以得到每个点的h(p)了。
第一种方法是a*+dijkstra
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <queue>
using namespace std;
#define maxn 111111
#define inf 0x1f1f1f1f
int head[maxn], head1[maxn], ecnt1, ecnt2;
int dist[maxn];
bool vis[maxn];
int sta, end;
struct edge
{
int v, t, next;
edge(){}
edge( int _v, int _t)
{
v = _v;
t = _t;
}
}e[maxn], e1[maxn];
void init()
{
memset(head, -1, sizeof(head));
memset(head1, -1, sizeof(head1));
ecnt1 = ecnt2 = 0;
}
void addedge( int u, int v, int t)
{
e[ecnt1] = edge(v,t);
e[ecnt1].next = head[u];
head[u] = ecnt1++;
e1[ecnt2] = edge(u,t);
e1[ecnt2].next = head1[v];
head1[v] = ecnt2++;
}
struct point
{
int v, g;
point(){};
point(int _v, int _g)
{
v = _v;
g = _g;
}
bool operator <(const point &a) const
{
return dist[v] + g > dist[a.v] + a.g;
}
};
priority_queue<point> que;
void dij( int sour)
{
memset(dist, inf, sizeof(dist));
memset(vis, 0, sizeof(vis));
dist[sour] = 0;
while(!que.empty()) que.pop();
point now ;
now = point(sour,0);
que.push(now);
point tem;
while(!que.empty())
{
now = que.top();
que.pop();
if(vis[now.v])
continue;
vis[now.v] = true;
for( int i = head1[now.v]; i != -1; i = e1[i].next)
{
int t = e1[i].v;
int cost = e1[i].t;
if(dist[t] > dist[now.v] + cost)
{
dist[t] = dist[now.v] + cost;
que.push(point(t,0));
}
}
}
}
int a_start( int k)
{
while(!que.empty()) que.pop();
point now, tem;
now = point(sta, 0);
que.push(now);
while(!que.empty())
{
now = que.top();
que.pop();
if(now.v == end)
{
if(k > 1)
k--;
else
return now.g;
}
for( int i = head[now.v]; i != -1; i = e[i].next)
{
que.push(point(e[i].v,e[i].t + now.g));
}
}
return -1;
}
int main()
{
int n, m, k;
while(scanf("%d %d",&n, &m) != eof)
{
init();
int u, v, t;
for( int i = 0; i < m; i++ )
{
scanf("%d %d %d",&u, &v, &t);
addedge(u, v, t);
}
scanf("%d %d %d",&sta, &end, &k);
dij(end);
if(!dist[sta] == inf)
{
printf("-1\n");
continue;
}
if(sta == end)
k++;
printf("%d\n",a_start(k));
}
return 0;
}
第二种采用a*+spfa
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <queue>
#define maxn 1005
#define maxm 500005
#define inf 1000000000
using namespace std;
struct node
{
int v, w, next;
}edge[maxm], revedge[maxm];
struct a
{
int f, g, v;
bool operator <(const a a)const {
if(a.f == f) return a.g < g;
return a.f < f;
}
};
int e, vis[maxn], d[maxn], q[maxm * 5];
int head[maxn], revhead[maxn];
int n, m, s, t, k;
void init()
{
e = 0;
memset(head, -1, sizeof(head));
memset(revhead, -1, sizeof(revhead));
}
void insert(int x, int y, int w)
{
edge[e].v = y;
edge[e].w = w;
edge[e].next = head[x];
head[x] = e;
revedge[e].v = x;
revedge[e].w = w;
revedge[e].next =revhead[y];
revhead[y] = e++;
}
void spfa(int src)
{
for(int i = 1; i <= n; i++) d[i] = inf;
memset(vis, 0, sizeof(vis));
vis[src] = 0;
int h = 0, t = 1;
q[0] = src;
d[src] = 0;
while(h < t)
{
int u = q[h++];
vis[u] = 0;
for(int i = revhead[u] ; i != -1; i = revedge[i].next)
{
int v = revedge[i].v;
int w = revedge[i].w;
if(d[v] > d[u] + w)
{
d[v] = d[u] + w;
if(!vis[v])
{
q[t++] = v;
vis[v] = 1;
}
}
}
}
}
int astar(int src, int des)
{
int cnt = 0;
priority_queue<a>q;
if(src == des) k++;
if(d[src] == inf) return -1;
a t, tt;
t.v = src, t.g = 0, t.f = t.g + d[src];
q.push(t);
while(!q.empty())
{
tt = q.top();
q.pop();
if(tt.v == des)
{
cnt++;
if(cnt == k) return tt.g;
}
for(int i = head[tt.v]; i != -1; i = edge[i].next)
{
t.v = edge[i].v;
t.g = tt.g + edge[i].w;
t.f = t.g + d[t.v];
q.push(t);
}
}
return -1;
}
int main()
{
int x, y, w;
while(scanf("%d%d", &n, &m) != eof)
{
init();
for(int i = 1; i <= m; i++)
{
scanf("%d%d%d", &x, &y, &w);
insert(x, y, w);
}
scanf("%d%d%d", &s, &t, &k);
spfa(t);
printf("%d\n", astar(s, t));
}
return 0;
}