搜索优化

算法简介

搜索是一种基本的算法，在建立一个搜索算法时，首先要考虑的问题其一是建立一个合适的算法模型，其二是选择合适的数据结构。然而，搜索方法的时间复杂度大多是指数级别的，简单而不加优化的搜索，其时间效率往往低的不能忍受。本章节所讨论的内容是在建立了合适的算法模型后，对程序进行了基本的优化。一个基本的优化就是剪枝。
搜索的过程可以看做是一个从树根出发，遍历一棵倒置的树，而所谓剪枝就是通过某种判断，避免一些不要的过程。应用剪枝优化的核心问题是设计剪枝判断方法，即确定哪些枝条应当舍弃，哪些枝条应当保留。并且剪枝算法应当遵守正确性，准确性，高效性。
怎样剪枝其具体判断视情况而定。应用比较灵活。下面有几种比较典型的方法。

α-β剪枝（极大极小搜索原理，常用于博弈）

为了提高搜索的效率，通过对值的上下限进行评估，从而减少需要进行评估节点的范围。

主要概念：

MAX节点的评估下限值α：作为MAX节点，假定它的MIN节点有N个，那么当它的第一个MIN节点的评估值为α时，则对于其它节点，如果有高于α的节点，就取那最高的节点值作为MAX节点的值；否则，该点的评估值为α。
MIN节点的评估上限值β：作为MIN节点，同样假定它的MAX节点有N个，那么当它的第一个MAX节点的评估值为β时，则对于其他节点，如果有低于β的节点，就取最低的节点值作为MIN节点的值；否则，该点的评估值为β 。

主要思想：

可以分为两个步骤，分别为α剪枝和β剪枝。
如图：
　　

参考：

《对弈程序基本技术》专题最小-最大搜索：http://www.xqbase.com/computer/search_minimax.htm
《对弈程序基本技术》专题 Alpha-Beta搜索：http://www.xqbase.com/computer/search_alphabeta.htm
Wikipedia MinMax ：http://en.wikipedia.org/wiki/Minimax
Wiki Alpha–beta pruning ：http://en.wikipedia.org/wiki/Alpha%E2%80%93beta_pruning
Minmax Explained：http://ai-depot.com/articles/minimax-explained/1/
讲解极小极大 (Minimax Explained) [译] ：http://www.starming.com/index.php?action=plugin&v=wave&tpl=union&ac=viewgrouppost&gid=34694&tid=15725
最小最大原理与搜索方法：http://blog.pfan.cn/rickone/16930.html

主要运用场合和思路

极大极小搜索策略一般都是使用在一些博弈类的游戏之中，这样策略本质上使用的是深度搜索策略，所以一般可以使用递归的方法来实现。在搜索过程中，对本方有利的搜索点上应该取极大值，而对本方不利的搜索点上应该取极小值。极小值和极大值都是相对而言的。在搜索过程中需要合理的控制搜索深度，搜索的深度越深，效率越低。

POJ 1568

问题：给出一个4x4 tic-tac-toe 的棋局的局面，问先手 "x" 是不是能找在接下来的一步中找到一个必胜局面，如果有，输出第一个落子位置（按顺序）。

#include <iostream>
using namespace std;
#define inf 100000000
int state[5][5],chess,xi,xj;
char ch;
int minfind(int,int,int);
int maxfind(int,int,int);
bool over(int x,int y) {
     bool flag = false;
     int row[5],col[5];
     memset(row,0,sizeof(row));
     memset(col,0,sizeof(col));
     for (int i=0;i<4;i++)
         for (int j=0;j<4;j++) {
             if (state[i][j]=='x') {
                row[i]++;
                col[j]++;
             }
             if (state[i][j]=='o') {
                row[i]--;
                col[j]--;
             }
         }
     if (row[x]==-4 || row[x]==4 || col[y]==-4 || col[y]==4)
        flag = true;
     int tot1 = 0, tot2 = 0;
     for (int i=0;i<4;i++) {
         if (state[i][i]=='x') tot1++;
         if (state[i][3-i]=='x') tot2++;
         if (state[i][i]=='o') tot1--;
         if (state[i][3-i]=='o') tot2--;
     }
     if ((tot1==4 || tot1==-4) && x==y)        flag = true;
     if ((tot2==4 || tot2==-4) && x==3-y)      flag = true;
     return flag;
}
int maxfind(int x,int y,int mini) {
    int tmp, maxi = -inf;
    if (over(x,y)) return maxi;
    if (chess==16) return 0;
    for (int i=0;i<4;i++)
        for (int j=0;j<4;j++)
            if (state[i][j]=='.') {
                       state[i][j]='x';
                       chess++;
                       tmp = minfind(i,j,maxi);
                       chess--;
                       state[i][j]='.';
                       maxi = max(maxi, tmp);
                       if (maxi>=mini) return maxi;
            }
    return maxi;
}
int minfind(int x,int y,int maxi) {
    int tmp, mini = inf;
    if (over(x,y)) return mini;
    if (chess==16) return 0;
    for (int i=0;i<4;i++)
        for (int j=0;j<4;j++)
            if (state[i][j]=='.') {
                       state[i][j]='o';
                       chess++;
                       tmp = maxfind(i,j,mini);
                       chess--;
                       state[i][j]='.';
                       mini = min(mini, tmp);
                       if (mini<=maxi) return mini;
            }
    return mini;
}
bool tryit() {
     int tmp, maxi = -inf;
     for (int i=0;i<4;i++)
         for (int j=0;j<4;j++)
             if (state[i][j]=='.') {
                state[i][j] = 'x';
                chess++;
                tmp = minfind(i,j,maxi);
                chess--;
                state[i][j] = '.';
                if (tmp>=maxi) {
                       maxi = tmp;
                       xi = i; xj = j;
                }
                if (maxi==inf) return true;
             }
     return false;
}
int main() {
    while (scanf("%c",&ch)) {
        if (ch=='$') break;
        scanf("%c",&ch);

        chess = -4;
        for (int i=0;i<4;i++)
            for (int j=0;j<5;j++) {
                scanf("%c",&state[i][j]);
                chess += state[i][j]!='.';
            }
        if (chess<=4) {  //强力剪枝
                      printf("#####\n");
                      continue;
        }
        if (tryit()) printf("(%d,%d)\n",xi,xj);
        else printf("#####\n");
    }
    return 0;
}

位运算剪枝

HDU 2553 N皇后问题

题意：n*n棋盘要放n个皇后，要求意2个皇后不允许处在同一排，同一列，也不允许处在与棋盘边框成45角的斜线上。最多几种方案

剪枝：

一个数和它的负数取与，得到的是最右边的1,负数在计算机里面的表示是原码取反加1.
按照行来进行枚举，同时将两个对角线和列的状态压缩表示。详细解释的话，我们可以这样想，对于任何一行，都有n个位置，那么这n个位置相应的列是否有皇后.
对于对角线，要单拿出来说一下。由于(i, j) (i+1, j-1)只能有一个值，而第i行的第一个位置，在主对角线的情况下对之后的行是没有影响的；同理，次对角线的情况，每一行的最后一个元素对于后面的行的是没有影响的，并且是第i行的第j个位置和i+1行的j+1的位置是对应。因此，在向下一层遍历的时候，要把主对角线向左进行移位，次对角线向右进行移位。这样，使得相应的位置可以对上。新增的置为0。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

int n, ans;
int limit;

void dfs( int h, int r, int l ) {
    if ( h == limit ) {  //说明n列都站满了
        ans++;
        return;
    }
    int pos = limit & (~(h|r|l)), p; //pos的二进制位0的，并且这个limit不能省，limit保证了pos高于n的位为0
    while ( pos ) {
        p = pos & (-pos); //这个运算，即原码和补码取与的运算，可以得出最右边的1；
        pos -= p;
        dfs( h+p, (r+p)<<1, (l+p)>>1 );
    }
}
int main()
{
    while ( scanf("%d", &n) != EOF && n ) {
        ans = 0;
        limit = ( 1<<n ) - 1; //limit的二进制是n个1；
        //cout << limit << endl;
        dfs( 0, 0, 0 );
        printf("%d\n", ans);
    }
}

奇偶剪枝

首先举个例子，有如下4*4的迷宫，'.'为可走路段，'X'为障碍不可通过
S...
....
....
...D
从S到D的最短距离为两点横坐标差的绝对值+两点纵坐标差的绝对值 = abs(Sx - Dx) + abs(Sy - Dy) = 6，这个应该是显而易见的。
遇到有障碍的时候呢？ S.XX
X.XX
...X
...D
你会发现不管你怎么绕路，最后从S到达D的距离都是最短距离+一个偶数，这个是可以证明的
而我们知道：
奇数 + 偶数 = 奇数
偶数 + 偶数 = 偶数
因此不管有多少障碍，不管绕多少路，只要能到达目的地，走过的距离必然是跟最短距离的奇偶性是一致的。
所以如果我们知道从S到D的最短距离为奇数，那么当且仅当给定的步数T为奇数时，才有可能走到。如果给定的T的奇偶性与最短距离的奇偶性不一致，那么我们就可以直接判定这条路线永远不可达了。
这里还有个小技巧，我们可以使用按位与运算来简化奇偶性的判断。我们知道1的二进制是1，而奇数的二进制最后一位一定是1，而偶数的二进制最后一位一定是0。所以如果数字&1的结果为1，那么数字为奇数，反之为偶数。

ZOJ Problem Set - 2110 Tempter of the Bone

题意：有一只狗要吃骨头，结果进入了一个迷宫陷阱，迷宫里每走过一个地板费时一秒，该地板就会在下一秒塌陷，所以你不能在该地板上逗留。迷宫里面有一个门，只能在特定的某一秒才能打开，让狗逃出去。现在题目告诉你迷宫的大小和门打开的时间，问你狗可不可以逃出去，可以就输出YES,否则NO。

思路：搜索+剪枝

如果当前时间即步数(step) >= T 而且还没有找到D点，则剪掉。
设当前位置(x, y)到D点(dx, dy)的最短距离为s，到达当前位置(x, y)已经花费时间(步数)step，那么，如果题目要求的时间T - step < s，则剪掉。
对于当前位置(x, y)，如果，(T-step-s)是奇数，则剪掉(奇偶剪枝)。
如果地图中，可走的点的数目(xnum) < 要求的时间T，则剪掉(路径剪枝)。

#include <iostream>
#include <cmath>
using namespace std;
int N, M, T, sx, sy, ex, ey;
char map[6][6];
const int dir[4][2] = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };
bool solved =  false, arrd[6][6];
int Distance ( int x, int y )
{
    return abs ( (double)x - ex ) + abs ( (double)y - ey ); // 当前点(x,y)到终点(ex,ey)的最短距离
}
void DFS ( int x, int y, int step )
{
    if ( solved ) return;
    if ( map[x][y] == 'D' && step == T ) {
        solved = true;
        return;
    }
    if ( step >= T ) return;                    // 当前时间即步数(step) >= T 而且还没有找到D点
    int dis = T - step - Distance ( x, y );
    if ( dis < 0 || dis % 2 ) return;           // 剩余步数小于最短距离或者满足奇偶剪枝条件
    for ( int i = 0; i < 4; i += 1 ) {
        int tx = x + dir[i][0];
        int ty = y + dir[i][1];
        int tstep = step + 1;
        if ( tx >= 0 && tx < N && ty >= 0 && ty < M && map[tx][ty] != 'X' && !arrd[tx][ty]) {
            arrd[tx][ty] = true;
            DFS ( tx, ty, tstep );
            arrd[tx][ty] = false;
        }
    }
}
int main ( int argc, char *argv[] )
{
    while ( cin >> N >> M >> T, N+M+T ) {
        solved = false;
        int xnum = 0;                           // 记录'X'的数量
        for ( int i = 0; i < N; i += 1 ) {
            cin.get();
            for ( int j = 0; j < M; j += 1 ) {
                cin >> map[i][j];
                arrd[i][j] = false;
                if ( map[i][j] == 'S' ) {
                    sx = i;
                    sy = j;
                    arrd[i][j] = true;
                }
                else if ( map[i][j] == 'D' ) {
                    ex = i;
                    ey = j;
                }
                else if ( map[i][j] == 'X' ) {
                    xnum++;
                }
            }
        }
        if ( N * M - xnum > T ) { // 可通行的点必须大于要求的步数，路径剪枝。
            DFS ( sx, sy, 0 );
        }
        if ( solved )
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
    return 0;
}

记忆化深度优先搜索

算法介绍

算法上依然是搜索的流程，但是搜索到的一些解用动态规划的那种思想和模式作一些保存。一般说来，动态规划总要遍历所有的状态，而搜索可以排除一些无效状态。更重要的是搜索还可以剪枝，可能剪去大量不必要的状态，因此在空间开销上往往比动态规划要低很多。
记忆化算法在求解的时候还是按着自顶向下的顺序，但是每求解一个状态，就将它的解保存下来，以后再次遇到这个状态的时候，就不必重新求解了。这种方法综合了搜索和动态规划两方面的优点，因而还是很有实用价值的。根据记忆化搜索的思想，它是解决重复计算，而不是重复生成，也就是说，这些搜索必须是在搜索扩展路径的过程中分步计算的题目，也就是“搜索答案与路径相关”的题目，而不能是搜索一个路径之后才能进行计算的题目，必须要分步计算，并且搜索过程中，一个搜索结果必须可以建立在同类型问题的结果上，也就是类似于动态规划解决的那种。
也就是说，他的问题表达，不是单纯生成一个走步方案，而是生成一个走步方案的代价等，而且每走一步，在搜索树/图中生成一个新状态，都可以精确计算出到此为止的费用，也就是，可以分步计算，这样才可以套用已经得到的答案一个公式简单地说：记忆化搜索=搜索的形式+动态规划的思想。

主要运用场合及思路

记忆化深度优先搜索

程序框架

const
  nonsense=-1; {这个值可以随意定义，表示一个状态的最优值未知}
var
…… {全局变量定义}

function work(s:statetype):longint;
var
…… {局部变量定义}
begin
  if opt[s]<>nonsense then
  begin
work:=opt[s];
exit;
end; {如果状态s的最优值已经知道，直接返回这个值}
枚举所有可以推出状态S的状态S1
begin
  temp:=由S1推出的S的最优值 {有关work(s1)的函数} ;
  if (opt[s]=nonsense) or (temp优于opt[s])
    then opt[s]:=temp;
end;
work:=opt[s]; {用动态规划的思想推出状态s的最优值}
end;

记忆化深度优先搜索采用了一般的深度优先搜索的递归结构，但是在搜索到一个未知的状态时它总把它记录下来，为以后的搜索节省了大量的时间。可见，记忆化搜索的实质是动态规划，效率也和动态规划接近；形式是搜索，简单易行，也不需要进行什么拓扑排序了。

hdu1078

题意：题意：老鼠偷吃，有n*n的方阵，每个格子里面放着一定数目的粮食，老鼠每次只能水平或竖直最多走k步，每次必须走食物比当前多的格子，问最多吃多少食物。
解题思路：记忆化搜索。

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;

int n,k,dp[105][105],a[105][105];
int to[4][2] = {1,0,-1,0,0,1,0,-1};

int check(int x,int y)
{
    if(x<1 || y<1 || x>n || y>n)
        return 1;
    return 0;
}

int dfs(int x,int y)
{
    int i,j,l,ans = 0;
    if(!dp[x][y])
    {
        for(i = 1; i<=k; i++)
        {
            for(j = 0; j<4; j++)
            {
                int xx = x+to[j][0]*i;
                int yy = y+to[j][1]*i;
                if(check(xx,yy))
                    continue;
                if(a[xx][yy]>a[x][y])
                    ans = max(ans,dfs(xx,yy));
            }
        }
        dp[x][y] = ans+a[x][y];
    }
    return dp[x][y];
}

int main()
{
    int i,j;
    while(~scanf("%d%d",&n,&k),n>0&&k>0)
    {
        for(i = 1; i<=n; i++)
            for(j = 1; j<=n; j++)
                scanf("%d",&a[i][j]);
        memset(dp,0,sizeof(dp));
        printf("%d\n",dfs(1,1));
    }

    return 0;
}

UVa 10118 Free Candies（记忆化搜索经典）

题意：
有4堆糖果，每堆有n（最多40）个，有一个篮子，最多装5个糖果，我们每次只能从某一堆糖果里拿出一个糖果，如果篮子里有两个相同的糖果，那么就可以把这两个（一对）糖果放进自己的口袋里，问最多能拿走多少对糖果。糖果种类最多20种.

思路：

这一题有点逆向思维的味道，dp[a, b, c, d] 表示从每堆中分别拿 a, b, c, d 个时，最多能拿多少个糖果;
注意一点：当拿到 a, b, c, d 时，不能再拿了，此时结果肯定就会固定。利用这一点性质，采用记忆化搜索能有效的减少重复子结构的计算;
题目是只有 0 0 0 0 这一个出发点的，根据这个出发点进行深搜，最终得出结果。
本题可谓是深搜 + 记忆化搜索的经典，状态不是那么明显，子结构也不是那么好抽象，因为转移的末状态并不是固定的，是在不断的搜索中求出来的;

#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cstdio>
using namespace std;

const int MAXN = 41;
int pile[4][MAXN], dp[MAXN][MAXN][MAXN][MAXN];
int n, top[4];

int dfs(int count, bool hash[]) {
    if (dp[top[0]][top[1]][top[2]][top[3]] != -1)
        return dp[top[0]][top[1]][top[2]][top[3]];

    if (count == 5)
        return dp[top[0]][top[1]][top[2]][top[3]] = 0;

    int ans = 0;
    for (int i = 0; i < 4; i++) {
        if (top[i] == n) continue;
        int color = pile[i][top[i]];
        top[i] += 1;
        if (hash[color]) {
            hash[color] = false;
            ans = max(ans, dfs(count-1, hash) + 1);
            hash[color] = true;
        } else {
            hash[color] = true;
            ans = max(ans, dfs(count+1, hash));
            hash[color] = false;
        }
        top[i] -= 1;
    }
    return dp[top[0]][top[1]][top[2]][top[3]] = ans;
}

int main() {
    while (scanf("%d", &n) && n) {
        for (int i = 0; i < n; i++)
            for (int j = 0; j < 4; j++)
                scanf("%d", &pile[j][i]);
        bool hash[25];
        memset(dp, -1, sizeof(dp));
        memset(hash, false, sizeof(hash));
        top[0] = top[1] = top[2] = top[3] = 0;
        printf("%d\n", dfs(0, hash));
    }
    return 0;
}

记忆化宽度优先搜索

程序框架

边界条件进入队列
找到一个没有扩展过的且肯定是最优的状态，没有则退出
扩展该状态，并修改扩展到的最优值
返回到第二步

记忆化宽度优先搜索实际上是把一般的动态规划倒过来了。动态规划在计算每一个状态的最优值时，总是寻找可以推出该状态的已知状态，然后从中选择一个最优的决策。而记忆化宽度优先搜索是不断地从已知状态出发，看看能推出哪些其它的状态，并修改其它状态的最优值。

这个算法有两大优点：

与记忆化深度优先搜索相似，避免了对错综复杂的拓扑关系的分析
化倒推为顺推，更加符合人类的思维过程，而且在顺推比倒推简单时，可以使问题简单化

例子

下面我们通过一个例子，具体问题具体分析

[问题描述]

司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），也可能是平原（用“P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

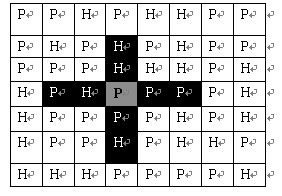
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。
数据限制：N<=100 M<=10

[算法分析]

这一题目若用图论的模型来做，就是一个最大独立集问题，而最大独立集问题确实一个NP问题。并且我们也做过这种题目的原型题目，大部分都必须通过搜索来解决。故我们需要考察这个问题的特殊性。
由数据限制可知mmax<<nmax。注意这是唯一一个与原型题目不同的地方。可是如何使用呢？我们先考虑一种极端情况，例如m=1的情况。这个时候，我们可以用如下的动态规划方程来解出结果：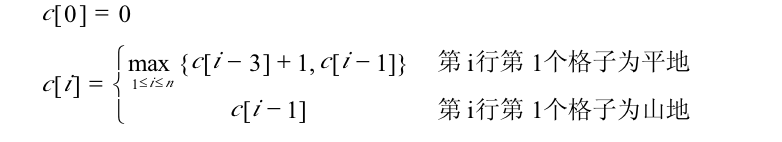

其中c[i]的含义是在前i行各自中可以放置的最多炮兵数，c[n]即为解答。

这种方法是否可以扩展到m列呢？
我们这时用c[i]表示m列时在前i行格子中可以放置的最多炮兵数。然后把每一行可能放置炮兵的方法求出来，然后就可以只考虑行与行之间放置炮兵的关系了。不过这样我们还是无法写出规划方程。观察这个时候情况与m=1式情况的不同：就是对于每以列我们多需要保存各自的c[i-3]和c[i-1]。有鉴于此，我们需要增设一个参数p来满足动态规划的需要。这里p应是一个m位的数组，并且每一位都有三种选择，第k列的三种选择分别代表该列取c[i-1]、c[i-2]、c[i-3]时所对应的最值。

这样，我们有：

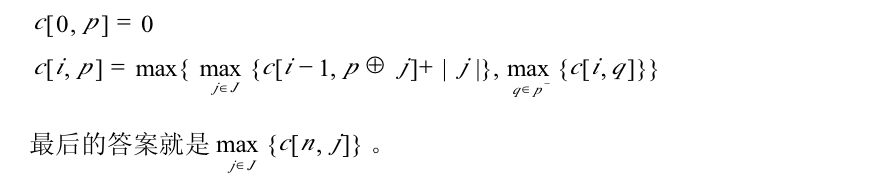我们虽然写出了状态转移方程式，但是如果用这样的方程式进行动态规划，实现起来是非常烦琐的，尤其涉及到了参数p的倒推，颇为复杂。于是我们又将目光投向了记忆化搜索——化倒推为顺推。把算法进行一些修改：c[0,p]为边界状态；以阵地的行作为阶段进行搜索，从c[I,p]推出所有c[I+1,p]，再从c[I+1,p]推出c[I+2,p]，……，直到c[n,p]。这样，使用记忆化搜索使得问题得到了圆满的解决！

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;

const int MAXN=105;

int N,M,sum,ans;
int now[MAXN],a[MAXN],b[MAXN],f[MAXN][MAXN][MAXN];
char s[MAXN],ch;

void Init()
{
     scanf("%d%d\n",&N,&M);
     for (int i=1;i<=N;i++)
     {
         for (int j=1;j<=M;j++)
         {
             scanf("%c",&ch);
             if (ch=='H') now[i]+=1<<(M-j);
         }
         scanf("%c",&ch);
     }

}

void Change(int x)
{
     memset(s,0,sizeof(s));
     int len=0;
     while (x>0)
     {
           if (x%2==1) s[len++]='1'; else s[len++]='0';
           x/=2;
     }
     while (len<=M) s[len++]='0';
     //strrev(s);
     for (int i=0;i<M/2;i++) swap(s[i],s[M-1-i]);
}

void Solve()
{
     int temp;
     bool flag;
     for (int i=0;i<=(1<<M)-1;i++)
     {
         temp=0;
         flag=1;
         Change(i);
         for (int j=0;j<M;j++)
             if (s[j]=='1')
             {
                           if (j+1<=M && s[j+1]=='1') {flag=0;break;}
                           if (j+2<=M && s[j+2]=='1') {flag=0;break;}
                           temp++;
             }
         if (flag)
         {
                  a[++sum]=i;
                  b[sum]=temp;
         }
     }

     for (int i=1;i<=sum;i++)
         f[1][i][1]=b[i];
     for (int i=2;i<=N;i++)
         for (int k1=1;k1<=sum;k1++)
             for (int k2=1;k2<=sum;k2++)
                 if (((a[k1]&a[k2])==0) && ((a[k1]&now[i])==0) && ((a[k2]&now[i-1])==0))
                    for (int k3=1;k3<=sum;k3++)
                        if (((a[k1]&a[k3])==0) && ((a[k2]&a[k3])==0) && ((a[k3]&now[i-2])==0))
                           f[i][k1][k2]=max(f[i][k1][k2],f[i-1][k2][k3]+b[k1]);
     for (int i=1;i<=sum;i++)
         for (int j=1;j<=sum;j++)
             if (((a[i]&a[j])==0) && ((a[i]&now[N])==0) && ((a[j]&now[N-1])==0))
                ans=max(ans,f[N][i][j]);
     printf("%d\n",ans);
}

int main()
{
    Init();
    Solve();
    return 0;
}

小结一下：首先，在“m<=10”的启发下，找到了动态规划的算法，这是主要的一个步骤；其次，我们选择了记忆化搜索，使得算法的实现变得容易了许多，这也是不可或缺的一步。总而言之，记忆化宽度优先搜索将宽度优先搜索的结构和动态规划的思想有机地结合在一起，为我们的解题提供了一个新的途径。

搜索的优化

搜索优化

算法简介

α-β剪枝（极大极小搜索原理，常用于博弈）

主要概念：

主要思想：

参考：

主要运用场合和思路

POJ 1568

位运算剪枝

HDU 2553 N皇后问题

奇偶剪枝

ZOJ Problem Set - 2110 Tempter of the Bone

记忆化深度优先搜索

算法介绍

主要运用场合及思路

程序框架

hdu1078

UVa 10118 Free Candies（记忆化搜索经典）

记忆化宽度优先搜索

程序框架

例子

results matching ""

No results matching ""