割点和桥

在一个无向图中，如果删去一个点，这个图的连通度增加了，删去的这个点就是原图的一个割点；如果删掉一条边，这个图的连通度增加了，删掉的这条边就是原图的一个桥。
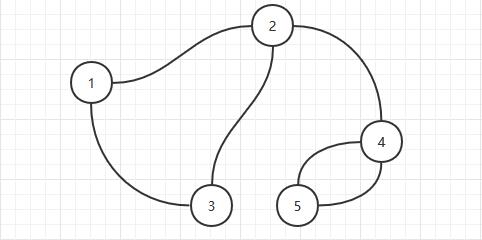
如图：

• 2，4号点是割点，去掉之后整个图分成了两个
• 2—4之间的边是桥，去掉之后整个图分成了两个

Hdu 3394.Railway

在一个有n个点，m条边的无向图中，如果某条边不在任何一个回路中，则称这条边是无用的如果某条边被多个回路利用，则称这条边是冲突的，求这个图中的冲突的和无用的边的条数

很明显，图中无用的边就是桥，而冲突的边呢？在每个块中，如果边数大于点数，那么这个块中的每条边都是冲突边。

#include <cstdio>
#include <cstring>
#include <vector>
#include <stack>
using namespace std;

#define MEM(a) memset(a, 0, sizeof(a))
#define pb push_back
const int maxv = 10000;
const int maxe = 100000;

struct Edge {
    int u, v;
    Edge () {}
    Edge (int a, int b ) {
        u = a;
        v = b;
    }
};

int pre[maxv], low[maxv], iscut[maxv], bccno[maxv];
int dfs_clock, bcc_cnt, qiao, ans2;
vector<int> G[maxe], bcc[maxv];
stack<Edge> S;

void dfs(int u, int fa) {
    low[u] = pre[u] = ++dfs_clock;

    for (int i = 0; i < (int)G[u].size(); i++) {
        int v = G[u][i];

        if (!pre[v]) {
            S.push(Edge(u,v));
            dfs(v, u);
            low[u] = min(low[u], low[v]);
            if (low[v] >= pre[u]) {
                if (low[v] > pre[u]) qiao++;
                bcc_cnt++; bcc[bcc_cnt].clear();
                for(;;) {
                    Edge x = S.top(); S.pop();
                    if (bccno[x.u] != bcc_cnt) {
                        bcc[bcc_cnt].push_back(x.u);
                        bccno[x.u] = bcc_cnt;
                    }
                    if (bccno[x.v] != bcc_cnt) {
                        bcc[bcc_cnt].push_back(x.v);
                        bccno[x.v] = bcc_cnt;
                    }
                    if (x.u == u && x.v == v) break;
                }
                int cnt2 = 0;
                for (int j = 0; j < (int)bcc[bcc_cnt].size(); j++) {
                    int k = bcc[bcc_cnt][j];
                    for (int h = 0; h < (int)G[k].size(); h++) {
                        int vv = G[k][h];
                        if (bccno[vv] == bcc_cnt) cnt2++;
                    }
                }
                if (cnt2/2 > (int)bcc[bcc_cnt].size()) ans2 += cnt2/2;
                cnt2 = 0;
            }
        } else if (pre[v] < pre[u] && v != fa) {
            S.push(Edge(u, v));
            low[u] = min(low[u], pre[v]);
        }
    }
}

void find_bcc(int n) {
    MEM(pre); MEM(iscut); MEM(bccno); MEM(low);
    dfs_clock = bcc_cnt = qiao = ans2 = 0;
    for (int i = 0; i < n; i++)
        if (!pre[i]) dfs(i, -1);
    for (int i = 0; i <= bcc_cnt; i++)
        bcc[i].clear();
}
int main() {
    //freopen("in.txt", "r", stdin);
    int n, m, u, v;
    while (scanf("%d%d", &n, &m) != EOF) {
        if (!n && !m) break;
        for (int i = 0; i < n; i++) G[i].clear();

        for (int i = 0; i < m; i++) {
            scanf("%d%d", &u, &v);
            G[u].pb(v); G[v].pb(u);
        }
        find_bcc(n);
        printf("%d %d\n", qiao, ans2);
    }        
    return 0;
}