线段

直线与线段的表示方法

我们可以用一条线段的两个端点来表示一条线段。直线的表示有两种方式，一种方式是使用二元一次方程$y=kx+b$来表示，另一种是用直线上任意一条长度不为零的线段来表示。由于使用方程表示接近垂直于某坐标轴的直线时容易产生精度误差，所以我们通常使用直线上的某条线段来表示直线。

struct Sg {
    Pt s, t;
    Sg() { }
    Sg(Pt s, Pt t) : s(s), t(t) { }
    Sg(double a, double b, double c, double d) : s(a, b), t(c, d) { }
};

点在线段上的判断

判断点$C$在线段$AB$上的两条依据：

1. $\vec{CA}\cdot\vec{CB} = 0$。
2. $C$在以$AB$为对角顶点的矩形内。

示例代码

bool PtOnSegment(Pt s, Pt t, Pt a) {
    return !det(a-s, a-t) && min(s.x, t.x) <= a.x && a.x <= max(s.x, t.x) &&
        min(s.y, t.y) <= a.y && a.y <= max(s.y, t.y);
}

另一种方法

判断点$C$在$AB$为对角线定点的矩形内较麻烦，可以直接判断$\vec{CA}\cdot\vec{CB}$的符号来判断$C$在直线$AB$上是否在$AB$之间。

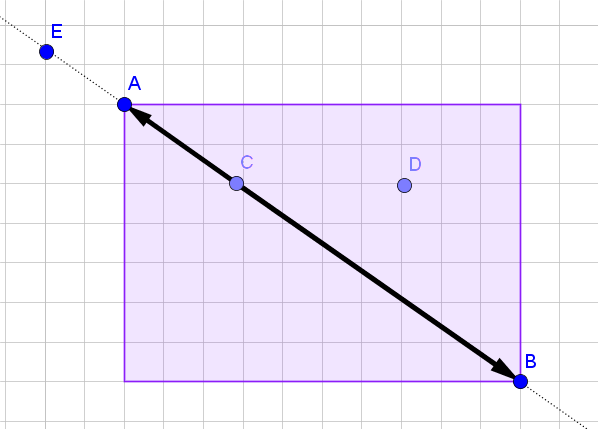
示例代码

bool PtOnSegment(Pt p, Pt a, Pt b) {
    return !sgn(det(p-a, b-a)) && sgn(dot(p-a, p-b)) <= 0;
}

把上例代码中的<=改成<就能实现不含线段端点的点在线段上的判断。

点在直线上的判断

点在直线上的判断很简单只要把点在线段上的判断的步骤2去掉即可。

示例代码

bool PtOnLine(Pt p, Pt s, Pt t) {
    return !sgn(det(p-a, b-a));
}

求点到直线的投影

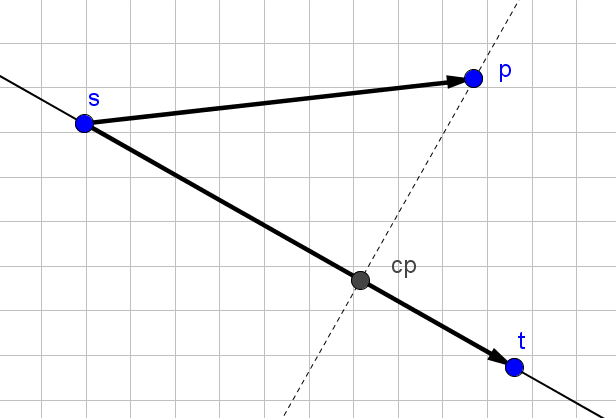
示例代码

Pt PtLineProj(Pt s, Pt t, Pt p) {
    double r = dot(p-s, t-s) / (t - s).norm();
    return s + (t - s) * r;
}

判断直线关系

直线有相交和平行两种关系，靠叉乘能简单判断。

bool parallel(Pt a, Pt b, Pt s, Pt t) {
    return !sgn(det(a-b, s-t));
}

判断线段关系

线段有相交和不相交两种关系，通常按照以下步骤判断。

1. 快速排斥试验
2. 跨立试验

快速排斥试验

设以线段$P_1P_2$为对角线的矩形为$R$，设以线段$Q_1Q_2$为对角线的矩形为$T$，如果$R$和$T$不相交，显然两线段不会相交。

跨立试验

如果两线段相交，则两线段必然相互跨立对方。若$P_1P_2$跨立$Q_1Q_2$，则矢量$\vec{Q_1P_1}$和$\vec{Q_1P_2}$位于矢量$\vec{Q_1Q_2}$的两侧，即$\vec{Q_1P_1} \times \vec{Q_1Q_2} \cdot \vec{Q_1Q_2} \times \vec{Q_1Q_2} < 0$。上式可改写成$\vec{Q_1P_1} \times \vec{Q_1Q_2} \cdot \vec{Q_1Q_2} \times \vec{Q_1P_2} > 0$。当$\vec{Q_1P_1} \times \vec{Q_1Q_2} = 0$时，说明$\vec{Q_1P_1}$和$\vec{Q_1Q_2}$共线，但是因为已经通过快速排斥试验，所以$P_1$一定在线段$Q_1Q_2$上；同理，$\vec{Q_1Q_2} \times \vec{Q_1P_2} = 0$说明$P_2$一定在线段$Q_1Q_2$上。所以判断$P_1P_2$跨立$Q_1Q_2$的依据是：$\vec{Q_1P_1} \times \vec{Q_1Q_2} \cdot \vec{Q_1Q_2} \times \vec{Q_1P_2} \geq 0$。同理判断$Q_1Q_2$跨立$P_1P_2$的依据是：$\vec{P_1Q_1} \times \vec{P_1P_2} \cdot \vec{P_1P_2} \times \vec{P_1Q_2} \geq 0$。

经典题目

• ZOJ 1648 Circuit Board
• POJ 3304 Segments
• POJ 2653 Pick-up sticks

求点到线段的距离

求线段$ab$到点p最短距离的方法为：

根据点$p$到的投影点的位置进行判断的方法：

1. 判断线段$pa$和$ab$所成的夹角，如果是钝角，那么$|pa|$是点到线段的最短距离。
2. 判断线段$pb$和$ab$所成的夹角，如果是钝角，那么$|pb|$是点到线段的最短距离。
3. 线段$pa$和线段$pb$与$ab$所成的夹角都不为钝角，那么点$p$到线段$ab$的距离是点$p$到直线$ab$的距离，这个距离可以用面积法直接算出来。

示例代码

double PtSegmentDist(Pt a, Pt b, Pt p) {
    if (sgn(dot(p-a, b-a)) <= 0) return (p-a).norm();
    if (sgn(dot(p-b, a-b)) <= 0) return (p-b).norm();
    return fabs(det(a-p, b-p)) / (a-b).norm();
}

经典题目

• URAL 1348 Goat in the Garden 2